コンテンツにスキップ

第10回 交流回路の複素ベクトル表現

今回は、三角関数を用いた交流の式が、複素静止ベクトルを用いた式に変換できることを示します。 複素ベクトルを簡単に説明したあとに、両者を結び付けます。 第9回の正弦波曲線と回転運動で示した内容を拡張したものになります。 回路図などはあまり登場しませんが、抵抗やコイル、コンデンサが接続された交流回路の解析に必須の方法（ツール）です。

なお、今回の講義資料は教科書と順番が大幅に異なっています。講義資料と教科書の対応が気になる人は、このページの下部の「教科書との対応について」を読んでみてください。また、複素数平面とベクトル表記はすでに習得していることを前提として、講義資料は作成されています。

正弦波曲線と計算の複雑さ

始めに、以下のような簡単な交流の回路を考えてみます。 これは、位相がπ2\frac{\pi}{2}°の異なる 2 つの 60MHz の交流電圧源が直列に接続されたものです。 交流電圧源も直流電圧源と同様に加算することで 1 つにまとめられるのですが、計算には三角関数の加法定理が必要になります。

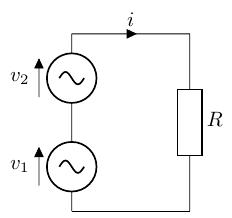
  • 交流電圧 v1=2V1sin⁡(ωt+θ1)v_1 = \sqrt{2} V_1 \sin (\omega t + \theta_1)
  • 交流電圧 v2=2V2sin⁡(ωt+θ2)v_2 = \sqrt{2} V_2 \sin (\omega t + \theta_2)
  • 合成電圧 v=v1+v2=2V1sin⁡(ωt+θ1)+2V2sin⁡(ωt+θ2)=2{V1(sin⁡ωt⋅cos⁡θ1+sin⁡θ1⋅cos⁡ωt)+V2(sin⁡ωt⋅cos⁡θ2+sin⁡θ2⋅cos⁡ωt)}=2{(V1cos⁡θ1+V2cos⁡θ2)sin⁡ωt+(V1sin⁡θ1+V2sin⁡θ2)cos⁡ωt}v = v_1 + v_2 = \sqrt{2} V_1 \sin (\omega t + \theta_1) + \sqrt{2} V_2 \sin (\omega t + \theta_2) = \sqrt{2} \left\{V_1 (\sin \omega t \cdot \cos \theta_1 + \sin \theta_1 \cdot \cos \omega t) + V_2 (\sin \omega t \cdot \cos \theta_2 + \sin \theta_2 \cdot \cos \omega t) \right\} = \sqrt{2} \left\{ (V_1 \cos \theta_1 + V_2 \cos \theta_2) \sin \omega t + (V_1 \sin \theta_1 + V_2 \sin \theta_2) \cos \omega t \right\}

位相がπ2\frac{\pi}{2}異なる2つの60MHzの交流電圧源の直列接続の回路のシミュレーション

第9回の正弦波曲線と回転運動で示したように、 下記の 2 つの図は、同じものを別の観点から見たものでした。 つまり、左の図は回転運動の図は、電圧と座標の関係を示したもので、右の図は正弦波曲線のグラフは、電圧と時刻の関係を図示したものでした。 電圧の変化は回転角ωt\omega t[rad]として、位相の変化はϕ\phiとして表されています。 なお、位相とは、とある 2 つの交流電圧源の時間方向の差分のことでした。


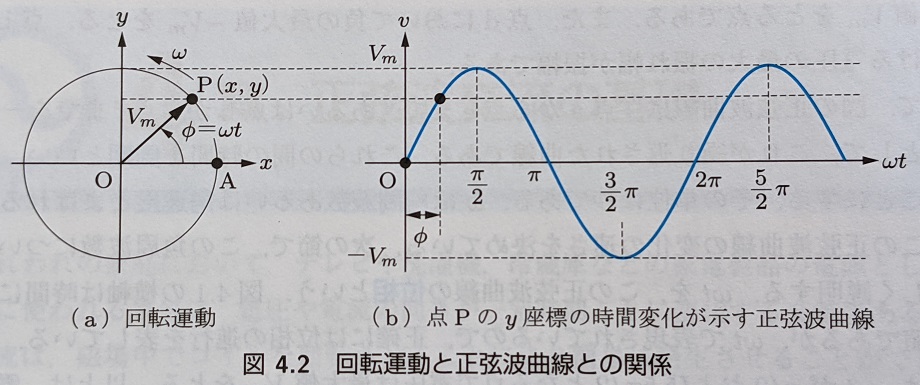
出典: 参考書 P.46

左の回転運動の図をxyxy平面ではなく、複素平面としてとらえます。 複素平面では、四則演算が代数的な計算のみによって行えます。 その反面、三角関数を用いた正弦波曲線の場合、加算をするだけでもsin⁡\sinの加算定理などが必要となり、計算が複雑になってしまいます。 両者は基本的に同じものですので、回路解析を複素平面のみで行うことで計算を簡単化できます。 これ実現するために考えられたのが、複素記号法です。 まずは、この方法を導入するための準備を行います。

複素ベクトルの基礎知識

ここでは、複素平面に登場するベクトルと、静止したベクトル、回転オペレータについて述べます。

複素ベクトル

複素平面を導入することで、回転運動は以下の 4 つの形式で表すことができます。 教科書では直交座標形式を多様しており、「複素ベクトル表記せよ」とある場合にも、直交座標形式が使われています。

  1. 直交座標形式: Z=a+jbZ = a + jb
  2. フェーザ形式: Z=r∠θZ = r \angle \theta
  3. 極座標形式: Z=r(cos⁡θ+sin⁡θ)Z = r (\cos \theta + \sin \theta)
  4. 指数関数形式: Z=rejθZ = r e^{j \theta}


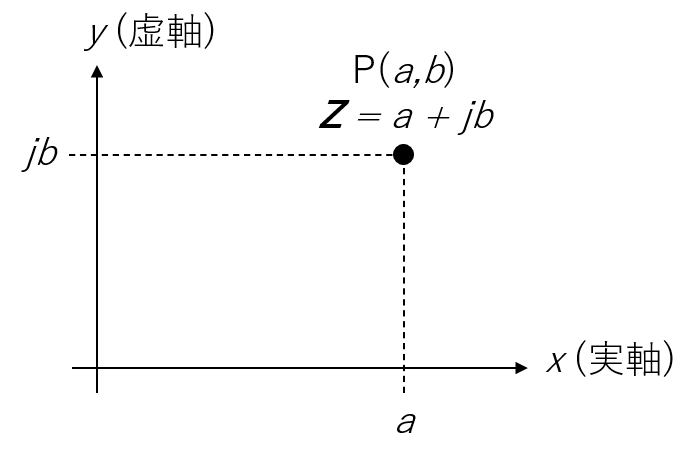
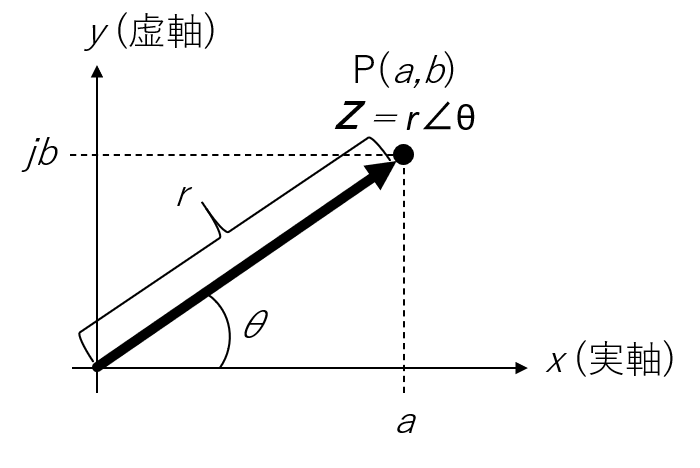
　　　　直交座標形式　　　　　　　　　　　　フェーザ形式

各表示形式を加減乗除をする際に使い分けると便利です。

  • 加減算は、直交座標形式を用いて、実部どうし、虚部どうしの足し算や引き算を行う。
  • 乗除算は、極座標形式か指数関数形式を用いて、絶対値はそれぞれ掛け算や割り算を、偏角はそれぞれ足し算や引き算を行う。

静止ベクトル

静止ベクトルとは、2 つのベクトルの位相の違いを複素ベクトルとして表現したものです。 基準とする複素ベクトルに対して、位相（のみ）がどのくらいズレているかを表すことができます。 2 つのベクトルが共通の角周波数で回転する場合、相対的な角度の関係は動いていないとみなせるからです。 なお、周波数は一緒であることが暗黙的に示されています。 周波数が変化する場合は、フェーザ図を用います。 本講義資料と教科書では、静止ベクトルをドットを使って表現しています。たとえば、E˙\dot{E}やI˙\dot{I}です。

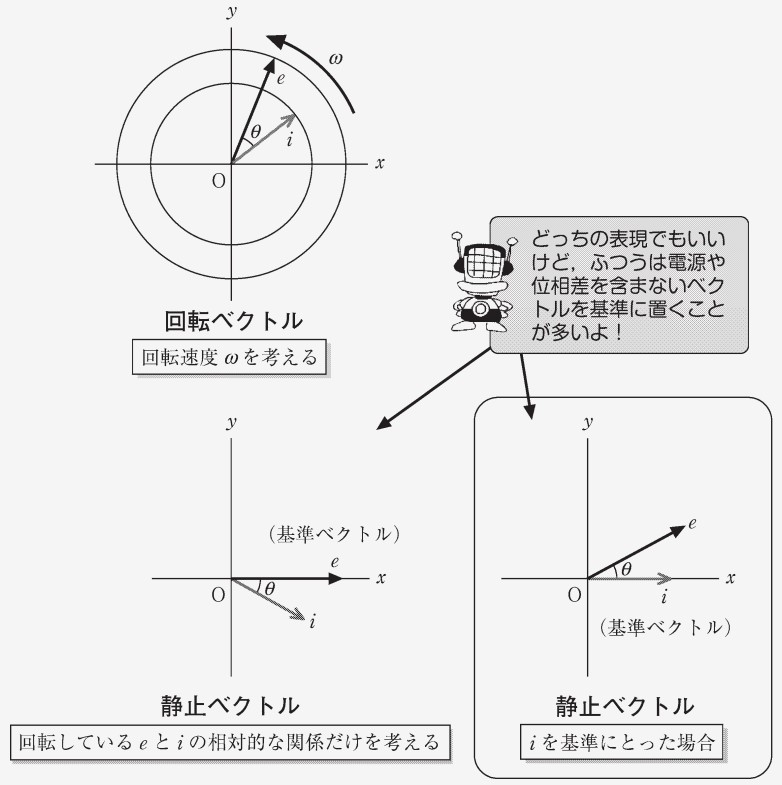
ベクトルの回転

とある複素数ZZに虚数jjを掛けると、以下のようになり、複素平面上では長さが一緒で角度が 90°反時計回りに回ったベクトルが描けます。

jZ=j(a+jb)=−b+jaj Z = j (a + jb) = - b + ja

これを複素ベクトルを用いて考えると、以下の表にまとめたことが言え、これを図示にしたものが下記の図になります。

正弦波曲線で位相を 複素平面上でベクトルを 極座標形式で
π2\frac{\pi}{2}[rad]だけ進める 90°だけ反時計回りに回す jjを掛ける
π2\frac{\pi}{2}[rad]だけ遅らせる 90°だけ時計回りに回す −j-jを掛ける

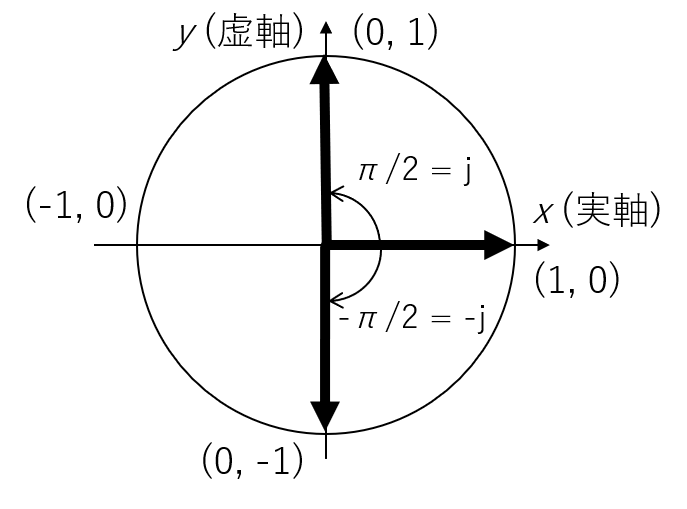
このように、jjを掛けることは、ベクトルを反時計回りに回転させる、回転オペレータとしての機能があることがわかります。 ですので、教科書の P.176 にあるように、jjには、位相をπ2\frac{\pi}{2}[rad]だけ進ませる機能があるんだ、という風に理解してください。 交流電源に接続されたコンデンサやコイルは、電流の位相をπ/2\pi/2だけ進めたり、遅らせたりするのですが、これらを表現するのに有用です。

演習問題

演習問題 8.1

次の複素数のベクトル図を描け。

  1. 4+3j4 + 3j
  2. 3−4j3 - 4j
  3. −5+3.44j-5 + 3.44j
  4. −3.44−5j-3.44 - 5j

演習問題 8.2

sin⁡θ\sin\thetaを基準ベクトルにとったとき、次の三角関数を複素ベクトルとして表現せよ。

  1. Asin⁡(θ+π3)A \sin(\theta + \frac{\pi}{3})
  2. Asin⁡(θ−π6)A \sin(\theta - \frac{\pi}{6})

演習問題 8.3

次の複素ベクトルを、基準ベクトルをsin⁡θ\sin \thetaとした三角関数として表現せよ。

  1. 5+53j5 + 5 \sqrt{3}j
  2. 7+7j7 + 7j

正弦波交流の複素数表示

ここからは、複素ベクトルを用いた交流回路の表現について見ていきます。 ある交流回路において、以下の式で表される交流電圧 eeと交流電流 iiがあったとします。

  • 交流電圧: e=2Eesin⁡(ωt)e = \sqrt{2} E_e \sin (\omega t) [V]
  • 交流電流: i=2Iesin⁡(ωt−π6)i = \sqrt{2} I_e \sin \left(\omega t - \frac{\pi}{6} \right) [A]

すると、この 2 つの電圧と電流には以下のことが言えます。

  • 周波数は、どちらも ωt\omega t[rad]で一緒
  • 位相は、電流iiが、電圧eeに対してπ6\frac{\pi}{6}[rad]だけ位相が遅れている(−π6-\frac{\pi}{6}なので)

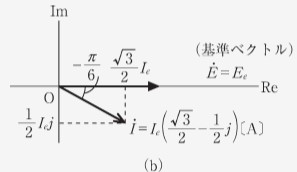
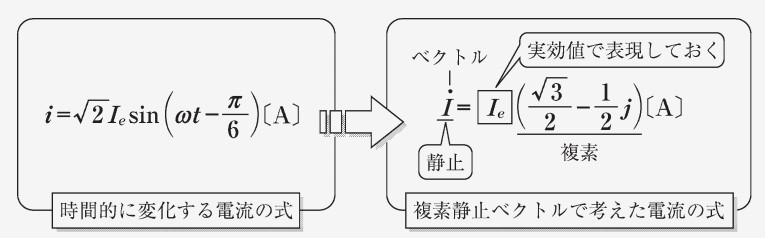
ここから、この 2 つを複素数の式と複素平面上の静止ベクトルとして表すと以下の式と図になります。 静止ベクトルですので、位相は異なりますが、周波数は同一なので無視できます。

  • 電圧: E˙=Ee\dot{E} = E_{e} [V]
  • 電流: I˙=Ie(32−12j)\dot{I} = I_{e} (\frac{\sqrt{3}}{2} - \frac{1}{2}j) [V]

ここまで、三角関数を用いた交流電圧/電流の式が、複素静止ベクトルを用いた式に等価変換できることが表せました。

簡単な解析例

最初の方で示した、交流電圧源が直列に接続された回路を複素ベクトルを用いて解析します。 計算できるように、電圧（実効値）をそれぞれV1e=103V_{1e} = 10\sqrt{3}, V2e=10V_{2e} = 10, 抵抗をR=10[Ω]R = 10[\Omega]と設定します。 この回路の合成電圧V′˙\dot{V'}と、抵抗に掛かる交流電流I˙\dot{I}を求めてみます。
なお、シミュレーション結果はここ にあります。

  • 交流電圧源 v1=2V1esin⁡(ωt)=2⋅103sin⁡(ωt)v_1 = \sqrt{2} V_{1e} \sin (\omega t) = \sqrt{2} \cdot 10\sqrt{3} \sin (\omega t)
  • 交流電圧源 v2=2V2esin⁡(ωt+π2)=2⋅10sin⁡(ωt+π2)v_2 = \sqrt{2} V_{2e} \sin (\omega t + \frac{\pi}{2}) = \sqrt{2} \cdot 10 \sin (\omega t + \frac{\pi}{2})

初めに、電圧の表記を複素ベクトル表記V1˙,V2˙\dot{V_1}, \dot{V_2}に直した回路図を示します。

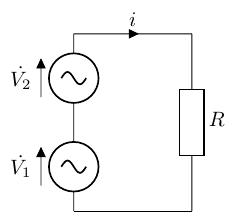
静止ベクトルを描く

2 つの電圧は、周波数が一緒で位相がπ2\frac{\pi}{2}異なるので、静止ベクトルが描けます。 具体的には、V1˙\dot{V_1}を基準ベクトルとして、V2˙\dot{V_2}を描くと、以下のようなベクトルになります。

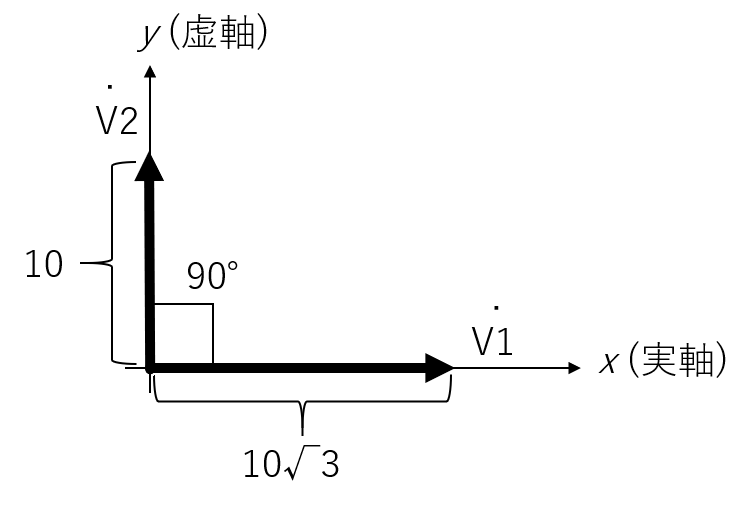
交流電圧を静止ベクトルの式で示す

  • 交流電圧 V1˙=V1e\dot{V_{1}} = V_{1e}
  • 交流電圧 V2˙=V2ej\dot{V_{2}} = V_{2e} j (V2e(cos⁡π2+jsin⁡π2)=V2eV_{2e}(\cos \frac{\pi}{2} + j \sin \frac{\pi}{2}) = V_{2e}なので)

合成電圧V′˙\dot{V'}を算出

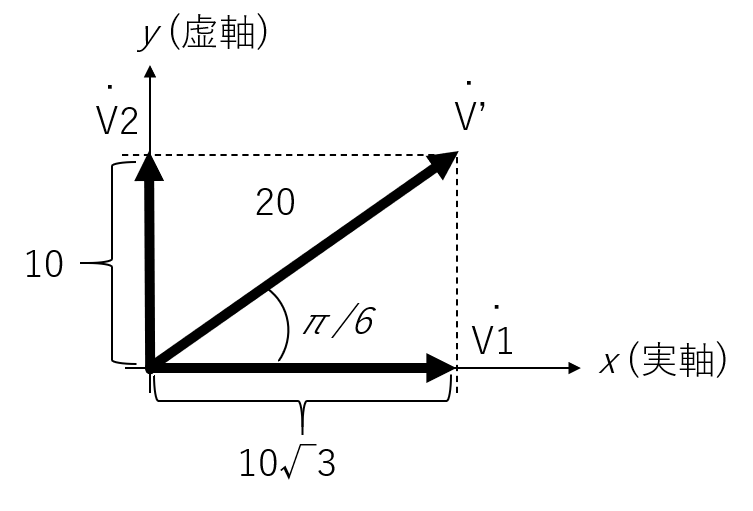
合成電圧の大きさと位相は、V1˙,V2˙\dot{V_1}, \dot{V_2}のベクトルの和になりますので、以下の式と図のようになります。

  • 交流電圧（複素ベクトル表記）V′˙=103+10j\dot{V'} = 10\sqrt{3} + 10j
  • 交流電圧の大きさ ∣V′∣˙=(103)2+102=20\dot{|V'|} = \sqrt{({10\sqrt{3}})^2 + {10}^2} = 20
  • 交流電圧（三角関数表記）v′=202sin⁡(ωt+π6)v' = 20\sqrt{2} \sin(\omega t + \frac{\pi}{6})

交流電流I˙\dot{I}

交流回路でも、抵抗に掛かる電流は位相は変化せず、オームの法則で求められます。（次回以降であらためてやります）

  • 電流の大きさ ∣I∣˙=∣V′∣˙R=2010=2\dot{|I|} = \frac{\dot{|V'|}}{R} = \frac{20}{10} = 2
  • 交流電流（複素ベクトル表記）I˙=3+1j\dot{I} = \sqrt{3} + 1j
  • 交流電流（三角関数表記）i=22sin⁡(ωt+π6)i = 2 \sqrt{2} \sin (\omega t + \frac{\pi}{6})

演習問題

演習問題 8.5

2 つの電圧の実効値が、E1e=100E_{1e} = 100[V], E2e=60E_{2e} = 60[V]で、その位相差はE2E_2がE1E_1よりもπ3\frac{\pi}{3}[rad]進んでいるものとすれば、その合成電圧EEの大きさはいくらになるか？

演習問題 8.7

答えが一部間違っているようです。2行目は以下のようになり、jjは要りません。

  • 誤：1R+j(ωC−1jωL)\frac{1}{R}+j(\omega C - \frac{1}{j \omega L})
  • 正：1R+j(ωC−1ωL)\frac{1}{R}+j(\omega C - \frac{1}{\omega L})

今回の講義資料と教科書の対応について

今回の講義資料は、本講義の教科書の第 8 章 P.168 8.3 節「 STEP 3 | 複素ベクトルを使って回路を解く」と、参考書 1『例題と演習で学ぶ電気回路』の「5 章交流の複素表現」をもとに作成されています。

教科書の第 7 章 「交流の計算」は、三角関数を用いて交流回路の解析を行い、そのたいへんさを説明するもので、非常に分かりやすくレアな内容です。 読み物として非常に有益ですので、ぜひ読んでみてください。 しかしながら、実際の回路解析に利用するのは三角関数ではなく複素ベクトルですので、いったんスキップします。 本講義の終わりの方で、抵抗やコイル、コンデンサが接続された回路を取り扱うときに、参考にします。

教科書の第 8 章の 8.1 節 「STEP 1 | 回転ベクトルと静止ベクトル」と、8.2 節は「虚数と複素数」は、STEP 3 で利用する数学的な知識の説明を行っている部分です。 本講義を受講する大多数のみなさんが、複素数平面とベクトル表記はすでに習得していると思われますので、この部分はスキップします。