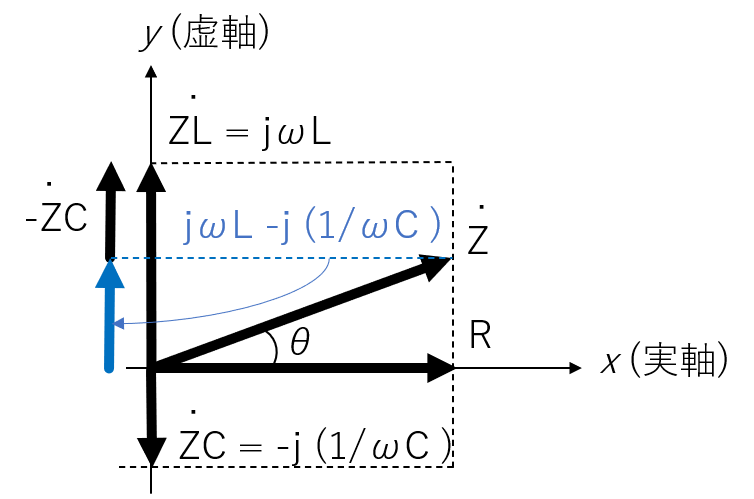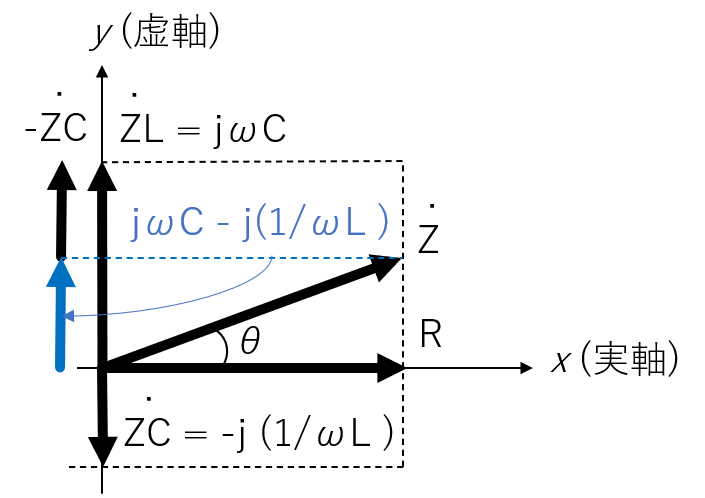コンテンツにスキップ

第12回 組み合わせ素子の交流回路

ここでは、いくつかの基本素子（抵抗、コイル、コンデンサ）を組み合わせた比較的単純な交流回路を取り扱います。 具体的には、交流電圧源と抵抗/コイル/コンデンサが直列や並列につながれた回路の挙動を解析します。 前回学んだ、交流電圧源と抵抗/コイル/コンデンサのみの回路から素子が増えた形です。回路解析自体は、手順に慣れてしまえば難しくありません。実際、本講義資料には、6 種類の回路が登場しますが、解析の手順はほぼすべて同一です。なお、回路解析には複素記号法のみを利用し、三角関数による解析は行いません。三角関数による回路解析の例は、教科書 P.148 の演習問題 7.1 などに載っています。

交流回路の解析には、抵抗、コイル、コンデンサの電流の複素ベクトル表記と電圧V˙\dot{V}に対する位相差を暗記していることが前提となります。前回示した、まとめの表を再掲します。

回路素子 電圧V˙\dot{V} 電流I˙\dot{I} I˙\dot{I}とV˙\dot{V}の位相差 インピーダンスZ˙\dot{Z}
抵抗 RR V˙=RI˙\dot{V} = R\dot{I} I˙=V˙R\dot{I} = \frac{\dot{V}}{R} 同相 レジスタンス RR
コイル LL V˙=jωLI˙\dot{V} = j \omega L \dot{I} I˙=−j1ωLV˙\dot{I} = -j \frac{1}{\omega L} \dot{V} 電流がπ2\frac{\pi}{2}遅れる 誘導性リアクタンス jωLj {\omega L}
コンデンサ CC V˙=−j1ωCI˙\dot{V} = -j \frac{1}{\omega C}\dot{I} I˙=jωCV˙\dot{I} = j \omega C \dot{V} 電流がπ2\frac{\pi}{2}進む 容量性リアクタンス −j1ωC-j \frac{1}{\omega C}

今回出てくる交流電圧源の式は、特に断りのない限り、以下のとおりとします。

  • 三角関数表記: v=Vmsin⁡(ωt)=2Vesin⁡(ωt)v = V_m \sin(\omega t) = \sqrt{2} V_{e} \sin (\omega t)
  • 複素ベクトル表記: V˙=Ve\dot{V} = V_{e}

なお、今回の講義資料は、本講義の参考書 1 の「第 7 章組み合わせ素子の交流回路」をもとに作成されています。

RL直列回路

以下のような、抵抗とコイルを正弦波交流電源に直列に接続した、RL 直列回路を考えます。また、RL直列回路のシミュレーション結果を示します。

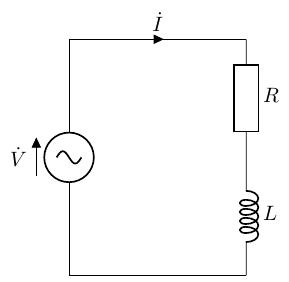
交流回路でも基本的な考え方は直列回路と変わらないことから、以下のような流れで解析できます。

解析手順

電流に関して

抵抗とコイルは直列に接続されているため、回路全体に流れる電流I˙\dot{I}はすべて同じものになります。また、 また、後述するインピーダンスZ˙\dot{Z}を用いて、電圧V˙\dot{V}と電流I˙\dot{I}の関係を表すこともでき、電圧に対して遅れた電流が流れることもわかります。

  • I˙=IR˙=IL˙=V˙Z˙=V˙R+jωL\displaystyle \dot{I} = \dot{I_R} = \dot{I_L} = \frac{\dot{V}}{\dot{Z}} = \frac{\dot{V}}{R + j \omega L}

また、電流の大きさ∣I˙∣|\dot{I}|は、以下のように求められます。

  • ∣I∣˙=∣V∣˙∣Z∣˙=∣V∣˙R2+(ωL)2\displaystyle \dot{|I|} = \frac{\dot{|V|}}{\dot{|Z|}} = \frac{\dot{|V|}}{\sqrt{R^2 + (\omega L)^2}}

電圧に関して

抵抗とコイルにかかる電圧VR˙\dot{V_R}とVL˙\dot{V_L}の電圧の合計はV˙\dot{V}となります。また、VR˙\dot{V_R}とVL˙\dot{V_L}は、まとめの表より、それぞれ電流I˙\dot{I}を使った形式で表せます。電流に対して進んだ電圧が印加されることもわかります。

  • V˙=VR˙+VL˙=RI˙+jωLI˙=(R+jωL)I˙\dot{V} = \dot{V_R} + \dot{V_L} = R \dot{I} + j \omega L \dot{I} = (R + j \omega L) \dot{I}

また、電圧の大きさ∣V˙∣|\dot{V}|は、以下のように求められます。

  • ∣V˙∣=R2+(ωL)2∣I∣˙|\dot{V}| = \sqrt{R^2 + (\omega L)^2}\dot{|I|}

回路のインピーダンス

電圧で導出した式と交流回路のオームの法則 V˙=Z˙I˙\dot{V} = \dot{Z} \dot{I}より、この回路のインピーダンスは以下のように導出できます。もちろん、直流回路と同様に、直列に接続されている回路素子の合成インピーダンスは、単純なインピーダンスの和として計算することもできます。

  • Z˙=(R+jωL)I˙I˙=R+jωL\displaystyle \dot{Z} = \frac{(R + j \omega L) \dot{I}}{\dot{I}} = R + j \omega L

また、インピーダンスの大きさ∣Z˙∣|\dot{Z}|は、以下のように導出できます。

  • ∣Z∣˙=R2+(ωL)2\displaystyle \dot{|Z|} = \sqrt{R^2 + (\omega L)^2}

ベクトル表記

電流を基準として、電圧を静止ベクトルで表すと、下記の左の図のようになります。以前学んだ様に、jjには位相をπ2\frac{\pi}{2}[rad]進ませる回転オペレータとしての機能があります。このとき、電圧の位相は以下のように求められます。

  • θ=tan⁡−1(∣VL˙∣∣VR˙∣)=tan⁡−1(ωLR)\displaystyle \theta = \tan^{-1}(\frac{|\dot{V_L}|}{|\dot{V_R}|}) = \tan^{-1}(\frac{\omega L}{R})

また、インピーダンスについても複素ベクトル表記ができ、下記の右の図になります。 このとき、位相差θ=tan⁡−1(ωLR)\theta = \tan^{-1}(\frac{\omega L}{R})となり、電圧の位相差と同じことがわかります。言い換えると、この回路の電圧の位相差はインピーダンスの位相差により決定される、ということになります。


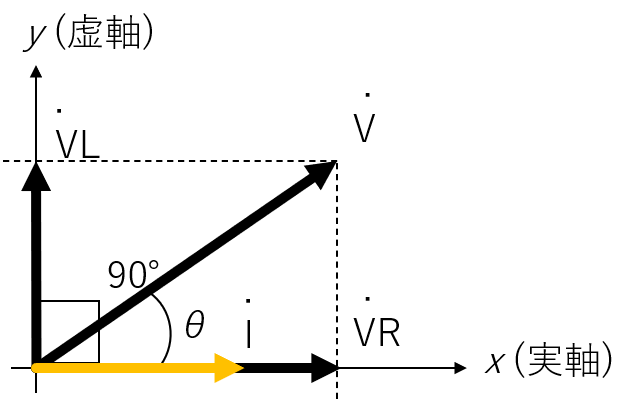
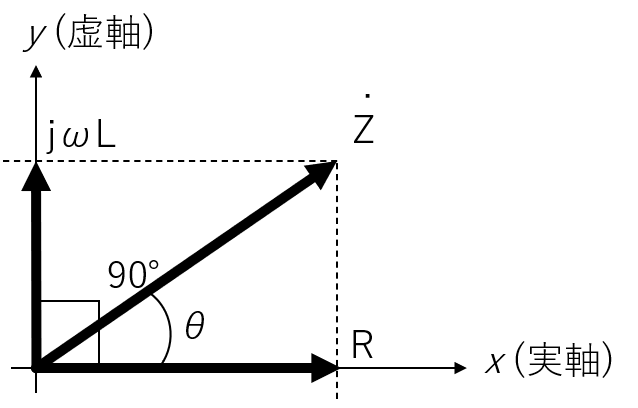
電圧と電流のベクトル表記と、インピーダンスのベクトル表記

その他

電流I˙\dot{I}と電圧V˙\dot{V}の位相差は、コイルと抵抗のインピーダンスの大きさによって変化することがわかります。 以下に、電圧と抵抗を固定して、コイルのインピーダンスのみを変化させたときの、電流のシミュレーション結果を示します。インピーダンスが大きくなるにつれて、位相差が大きくなっていることがわかります。

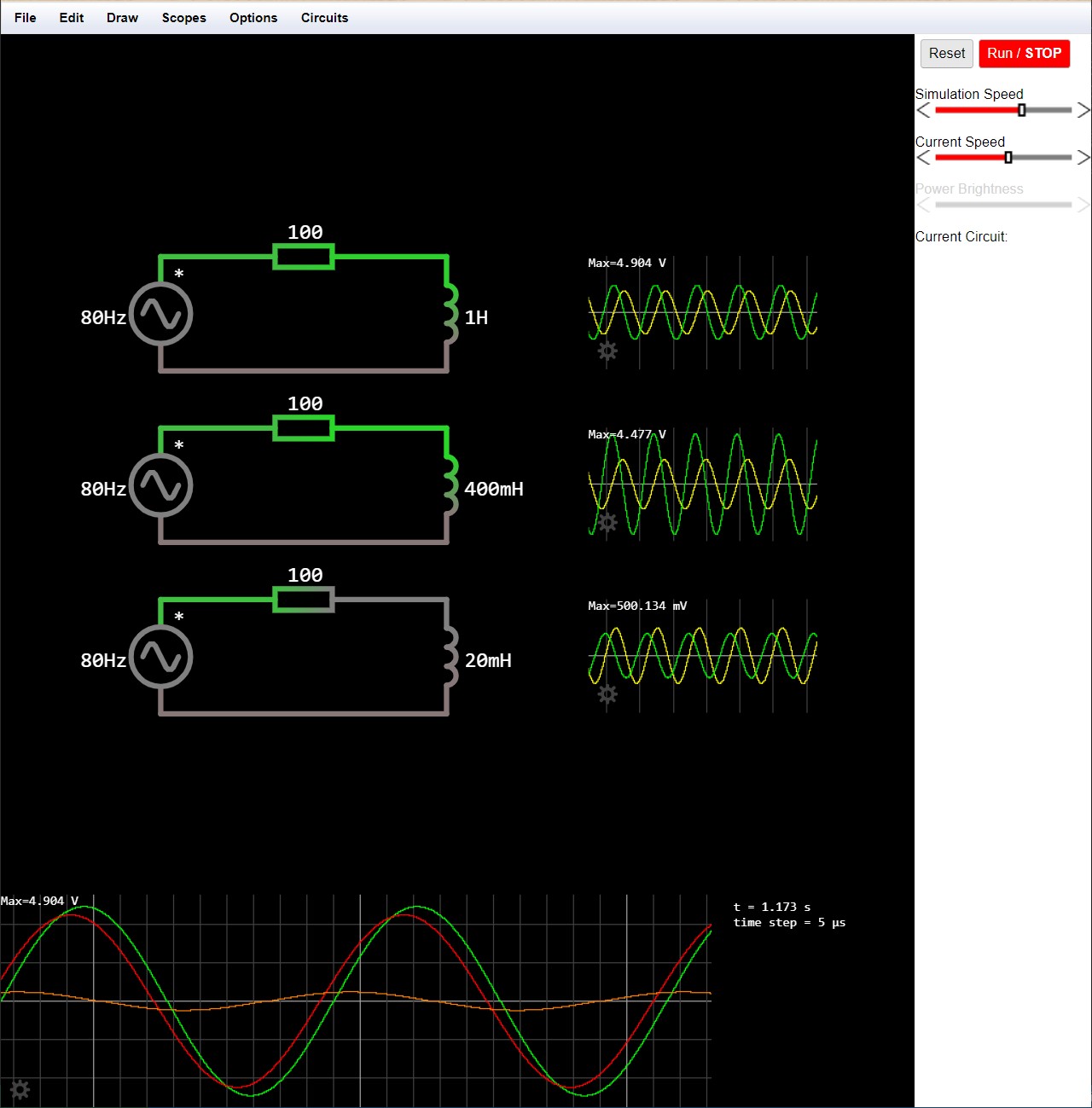
インダクタンスの違いによる電流の位相の変化のシミュレーション結果

演習問題

参考書 1 の P.82 例題 7.1
上記の RL 直列回路において、抵抗がRR=10[Ω\Omega]、インダクタンスがLL=20[mH]であった。この回路に実効値が 5[A]、角周波数ω\omega=300[rad/s]の交流電流が流れている。電流を基準としたときの、加えた電圧V˙\dot{V}を求めよ。また、複素平面上に回路のインピーダンスZ˙\dot{Z}と、電流および電圧の関係を図示せよ。

RC直列回路

以下のような、抵抗とコンデンサを正弦波交流電源に直列に接続した、RC 直列回路を考えます。また、RC直列回路のシミュレーション結果を示します。

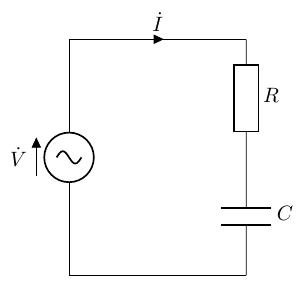
RC 直列回路でも、交流回路でも基本的な考え方は直列回路と変わらないことから、以下のような流れで解析できます。

解析手順

電流に関して

抵抗とコイルは直列に接続されているため、回路全体に流れる電流I˙\dot{I}はすべて同じものになります。また、後述するインピーダンスZ˙\dot{Z}を用いて、電圧V˙\dot{V}と電流I˙\dot{I}の関係を表すこともでき、電圧に対して進んだ電流が流れることもわかります。

  • I˙=IR˙=IC˙=V˙Z˙=V˙R−j1ωC\displaystyle \dot{I} = \dot{I_R} = \dot{I_C} = \frac{\dot{V}}{\dot{Z}} = \frac{\dot{V}}{R - j \frac{1}{\omega C}}

また、電流の大きさ∣I˙∣|\dot{I}|は、以下のように求められます。

  • ∣I∣˙=∣IR∣˙=∣IC∣˙=∣V∣˙∣Z∣˙=∣V∣˙R2+(1ωC)2\displaystyle \dot{|I|} = \dot{|I_R|} = \dot{|I_C|} = \frac{\dot{|V|}}{\dot{|Z|}}= \frac{\dot{|V|}}{\sqrt{R^2 + (\frac{1}{\omega C})^2}}

電圧に関して

抵抗とコイルにかかる電圧VR˙\dot{V_R}とVC˙\dot{V_C}の電圧の合計はV˙\dot{V}となります。また、VR˙\dot{V_R}とVC˙\dot{V_C}は、まとめの表より、それぞれ電流I˙\dot{I}を使った形式で表せます。また、電流に対して遅れた電圧が流れることもわかります。

  • V˙=VR˙+VC˙=RI˙−j1ωCI˙=(R−j1ωC)I˙\dot{V} = \dot{V_R} + \dot{V_C} = R \dot{I} - j \frac{1}{\omega C} \dot{I} = (R - j \frac{1}{\omega C}) \dot{I}

また、電圧の大きさ∣V˙∣|\dot{V}|は、以下のように求められます。

  • ∣V˙∣=∣VR˙∣2+∣VC˙∣2I˙=R2+(1ωC)2∣I∣˙|\dot{V}| = \sqrt{|\dot{V_R}|^2 + |\dot{V_C}|^2} \dot{I} = \sqrt{R^2 + (\frac{1}{\omega C})^2} \dot{|I|}

回路のインピーダンス

電圧で導出した式と交流回路のオームの法則 V˙=Z˙I˙\dot{V} = \dot{Z} \dot{I}より、この回路のインピーダンスは以下のように求められます。もちろん、直流回路と同様に、直列に接続されている回路素子の合成インピーダンスは、単純なインピーダンスの和として計算することもできます。

  • Z˙=V˙I˙=(R−j1ωC)I˙I˙=R−j1ωC\displaystyle \dot{Z} = \frac{\dot{V}}{\dot{I}} = \frac{(R - j \frac{1}{\omega C}) \dot{I}}{\dot{I}} = R - j \frac{1}{\omega C}

また、インピーダンスの大きさ∣Z˙∣|\dot{Z}|は、以下のように求められます。

  • ∣Z˙∣=∣V∣˙∣I∣˙=R2+(1ωC)2\displaystyle |\dot{Z}| = \frac{\dot{|V|}}{\dot{|I|}} = \sqrt{R^2 + (\frac{1}{\omega C})^2}

ベクトル表記

電流を基準として、電圧を静止ベクトルで表すと、下記の左の図のようになります。このとき、電圧の位相は以下のように求められます。

  • θ=tan⁡−1(−∣VC˙∣∣VR˙∣)=tan⁡−1(−1ωCR)=tan⁡−1(−1ωCR)\displaystyle \theta = \tan^{-1}(\frac{-|\dot{V_C}|}{|\dot{V_R}|}) = \tan^{-1}(\frac{- \frac{1}{\omega C}}{R}) = \tan^{-1}(\frac{- 1}{\omega C R})

また、インピーダンスについても複素ベクトル表記ができ、下記の右の図になります。 このとき、位相差θ=tan⁡−1(1ωCR)\theta = \tan^{-1}(\frac{1}{\omega C R})となり、電圧の位相差と同じことがわかります。言い換えると、この回路の電圧の位相差はインピーダンスの位相差により決定される、ということになります。


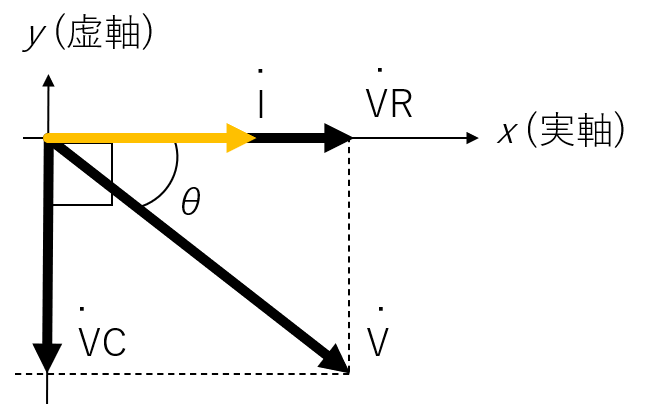
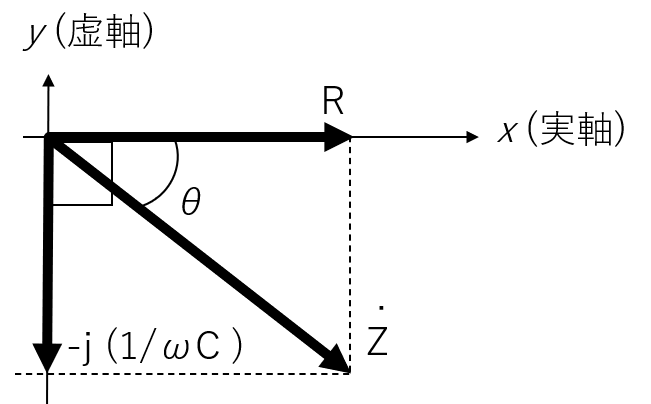
電圧と電流のベクトル表記と、インピーダンスのベクトル表記

その他

電流I˙\dot{I}と電圧V˙\dot{V}の位相差は、コンダクタと抵抗のインピーダンスの大きさによって変化することがわかります。 以下に、電圧と抵抗を固定して、コンダクタのインピーダンスのみを変化させたときの、電流のシミュレーション結果を示します。インピーダンスが大きくなるにつれて、位相差が大きくなっていることがわかります。

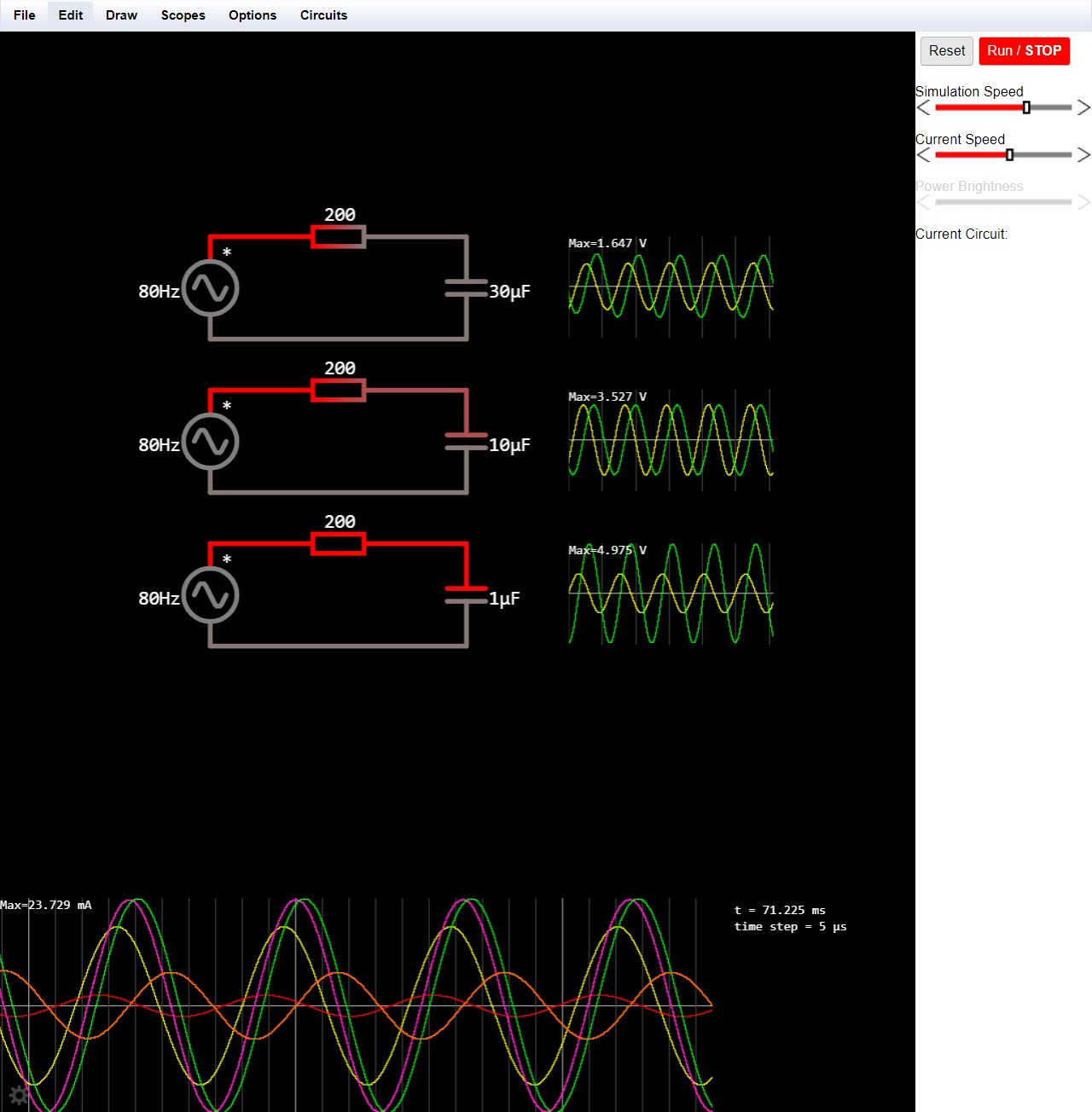
キャパシタンスの違いによる電流の位相の変化のシミュレーション結果

演習問題

参考書 1 の P.85 例題 7.2
上記の RL 直列回路において、抵抗がRR=5[Ω\Omega]、キャパシタンスがCC=200[μ\muF]であった。この回路に実効値が 100[V]、角周波数ω\omega=500[rad/s]の交流電圧を加えた。電圧を基準としたときの、この回路に流れる電流の実効値と偏角を求めよ。また、複素平面上に回路のインピーダンスZ˙\dot{Z}と、電流および電圧の関係を図示せよ。

RLC直列回路

以下のような、抵抗とコイルとコンデンサを正弦波交流電源に直列に接続した、RLC 直列回路を考えます。また、RLC直列回路のシミュレーション結果を示します。

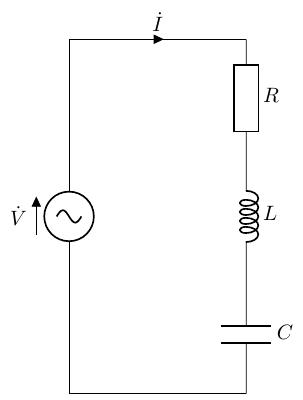
RL 直列回路や RC 直列回路と同様に、以下のような流れで解析できます。

解析手順

電流に関して

抵抗とコイル、コンデンサは直列に接続されているため、回路全体に流れる電流I˙\dot{I}はすべて同じものになります。また、後述するインピーダンスZ˙\dot{Z}を用いて、電圧V˙\dot{V}と電流I˙\dot{I}の関係を表すこともできます。この式を見てみると、電流と電圧の位相の関係は、コイルとコンデンサのインピーダンスの大小によって決まる、と言えます。

  • I˙=IR˙=IL˙=IC˙=V˙Z˙=V˙R+j(ωL−1ωC)\displaystyle \dot{I} = \dot{I_R} = \dot{I_L} = \dot{I_C} = \frac{\dot{V}}{\dot{Z}} = \frac{\dot{V}}{R + j (\omega L - \frac{1}{\omega C})}

また、電流の大きさ∣I˙∣|\dot{I}|は、以下のように求められます。

  • ∣I∣˙=∣V∣˙∣Z∣˙=∣V∣˙R2+(ωL−1ωC)2\displaystyle \dot{|I|} = \frac{\dot{|V|}}{\dot{|Z|}} = \frac{\dot{|V|}}{\sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2}}

電圧に関して

抵抗とコイル、コンデンサにかかる電圧VR˙\dot{V_R}とVL˙\dot{V_L}、VC˙\dot{V_C}の電圧の合計がV˙\dot{V}となります。また、VR˙\dot{V_R}とVL˙\dot{V_L}、VC˙\dot{V_C}は、まとめの表より、それぞれ電流I˙\dot{I}を使った形式で表せます。

  • V˙=VR˙+VL˙+VC˙=RI˙+jωLI˙−j1ωCI˙=(R+j(ωL−1ωC))I˙\dot{V} = \dot{V_R} + \dot{V_L} + \dot{V_C}= R \dot{I} + j \omega L \dot{I} - j \frac{1}{\omega C} \dot{I} = (R + j (\omega L - \frac{1}{\omega C})) \dot{I}

また、電圧の大きさ∣V˙∣|\dot{V}|は、以下のように求められます。

  • ∣V˙∣=R2+(ωL−1ωC)2∣I∣˙|\dot{V}| = \sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2}\dot{|I|}

回路のインピーダンス

電圧で導出した式と交流回路のオームの法則 V˙=Z˙I˙\dot{V} = \dot{Z} \dot{I}より、この回路のインピーダンスは以下のように求められます。もちろん、直流回路と同様に、直列に接続されている回路素子の合成インピーダンスは、単純なインピーダンスの和として計算することもできます。

  • Z˙=V˙I˙=(R+jωL−j1ωC)I˙I˙=R+j(ωL−1ωC)\displaystyle \dot{Z} = \frac{\dot{V}}{\dot{I}} = \frac{(R + j \omega L - j \frac{1}{\omega C}) \dot{I}}{\dot{I}} = R + j (\omega L - \frac{1}{\omega C})

また、インピーダンスの大きさ∣Z˙∣|\dot{Z}|は、以下のように求められます。

  • ∣Z˙∣=R2+(ωL−1ωC)2\displaystyle |\dot{Z}| = \sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2}

ベクトル表記

電流を基準として、電圧を静止ベクトルで表すと、下記の左の図のようになります。3 つのベクトルの合成ですので、少し注意が必要です。電圧V˙\dot{V}の位相は、コイルのインピーダンスとコンデンサのインピーダンスの大小関係で変化すると言えます。

以下のサイトでは、Web ベースのツールでベクトルの合成を視覚的に表現できます。
Vector Addition - PhET: Free online physics, chemistry, biology, earth science and math simulations

また、このときの電圧の位相は以下のように求められます。

  • θ=tan⁡−1(∣VL˙∣−∣VC˙∣∣VR˙∣)=tan⁡−1(ωL−1ωCR)\displaystyle \theta = \tan^{-1}(\frac{|\dot{V_L}|-|\dot{V_C}|}{|\dot{V_R}|}) = \tan^{-1}(\frac{\omega L- \frac{1}{\omega C}}{R})

また、インピーダンスについても複素ベクトル表記ができ、下記の右の図になります。 このとき、位相差tan⁡−1(ωL−1ωCR)\tan^{-1}(\frac{\omega L - \frac{1}{\omega C}}{R})となり、電圧の位相差と同じことがわかります。


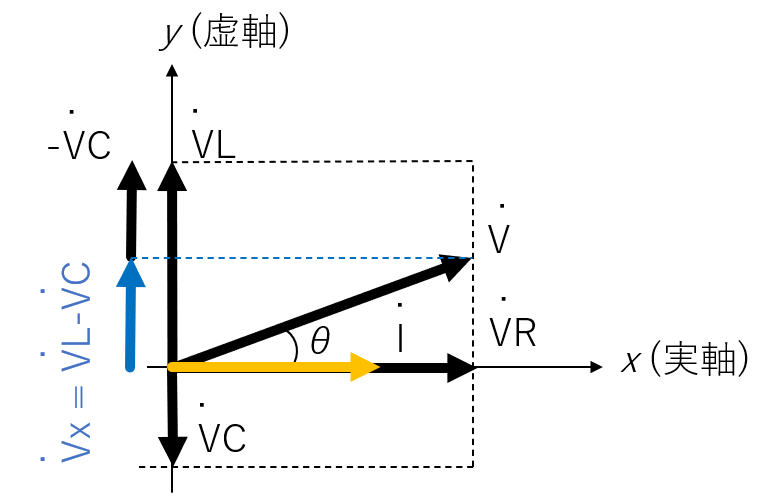
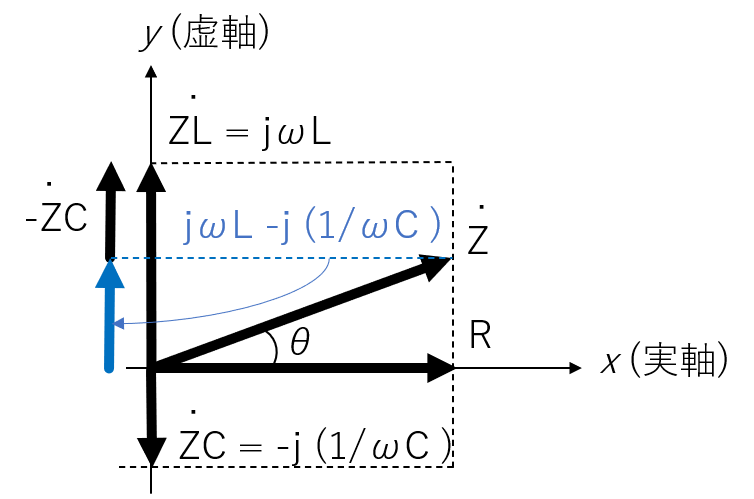
電圧と電流のベクトル表記と、インピーダンスのベクトル表記

その他

電圧V˙\dot{V}の位相は、コイルのリアクタンスXLX_LとコンデンサのリアクタンスXCX_Cの大小関係で変化することがわかりました。この 2 つのリアクタンスの大きさが一緒のとき、XL−XC=0X_L - X_C = 0となり、リアクタンス成分は最小、つまり零になります。その結果、電圧の位相も零となり、インピーダンスは抵抗だけとなります。このときこの回路に流れる電流の大きさが最大となり、この状態を共振と呼びます。

共振となるとき、以下のように式を展開でき、最終的に求められた角周波数ω\omegaを共振角周波数 ω0\omega_0と言います。

  • 共振角周波数: ω0→XL=XC\omega_0 \rightarrow X_L = X_C →\rightarrow ωL=1ωC\omega L = \frac{1}{\omega C} →\rightarrow ωL=1ωC\omega L = \frac{1}{\omega C} →\rightarrow ω=1LC=ω0\omega = \frac{1}{\sqrt{LC}} = \omega_0

また、ω=2πf\omega = 2 \pi fで角周波数を周波数に変換して、周波数で共振を表したものを共振周波数f0f_0と言います。

  • 共振周波数: f0→ω0=2πf0=1LCf_0 \rightarrow \omega_0 = 2 \pi f_0 = \frac{1}{\sqrt{LC}} →\rightarrow f0=12πLCf_0 = \frac{1}{2 \pi \sqrt{L C}}

以下に、交流電圧源の周波数を 31.8Hz とし、コイルのリアクタンスXLX_LとコンデンサのリアクタンスXCX_Cを変化させたときの RLC 直列回路のシミュレーション結果を示します。LL = 5[H], CC = 5[F]のときに共振状態となり、回路に流れる電流が最大となります。

共振しているRLC並列回路

演習問題

参考書 1 の P.88 例題 7.3
上記の RLC 直列回路において、抵抗がRR=5[Ω\Omega]、インダクタンスがLL=30[mH]、キャパシタンスCC=200[μ\muF]であった。この回路に瞬時値がi=102sin⁡500ti = 10 \sqrt{2}\sin500tで与えられる電流が流れている。この回路のインピーダンスZ˙\dot{Z}の大きさ、その偏角（位相）θ\theta、この回路に加えた電圧の瞬時値、各素子の電圧（降下）の実効値を求めよ。また、複素平面上に、電流を基準にしたときの、回路のインピーダンスZ˙\dot{Z}と、電流および各素子にかかる電圧の関係を示すフェーザ図を描け。

RL並列回路

以下のような、抵抗とコイルを正弦波交流電源に並列に接続した RL 並列回路を考えます。また、RL並列回路のシミュレーション結果を示します。

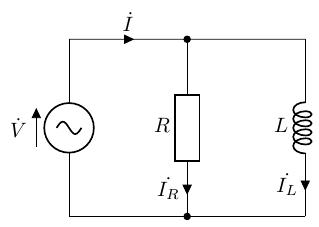
交流回路でも基本的な考え方は直列回路と変わらないことから、以下のような流れで解析できます。

解析手順

電圧に関して

抵抗とコイルは並列に接続されているため、両者に掛かる電圧V˙\dot{V}は一緒になります。また、後述するインピーダンスZ˙\dot{Z}を用いて、電圧V˙\dot{V}と電流I˙\dot{I}の関係を表すこともでき、電流に対して進んだ電圧が印加されることもわかります。

  • V˙=I˙Z˙=1(1R−j1ωL)I˙\displaystyle \dot{V} = \dot{I}\dot{Z} = \frac{1}{(\frac{1}{R} - j \frac{1}{\omega L})}\dot{I}

また、電圧の大きさ∣V˙∣|\dot{V}|は、以下のように求められます。

  • ∣V∣˙=∣I∣˙∣Z∣˙=1(1R)2+(1ωL)2∣I∣˙\displaystyle \dot{|V|} = \dot{|I|}\dot{|Z|} =\frac{1}{\sqrt{(\frac{1}{R})^2 + (\frac{1}{\omega L})^2}}\dot{|I|}

電流に関して

抵抗とコイルに流れる電流IR˙\dot{I_R}とIL˙\dot{I_L}について、キルヒホッフの電流則が成り立ちます。つまり、ある節点に流入する電流の総和と流出する電流の総和は等しいです。第3回 キルヒホッフの法則で学んだものがそのまま使えます。なお、コイルのインピーダンスはXL=jωLX_L = j \omega Lです。

  • 節点方程式: I˙=IR˙+IL˙\dot{I} = \dot{I_R} + \dot{I_L}
  • IR˙=V˙R\dot{I_R} = \frac{\dot{V}}{R}
  • IL˙=−j1ωLV˙\dot{I_L} = - j \frac{1}{\omega L} \dot{V}

電流I˙\dot{I}を電圧V˙\dot{V}を用いて表すと以下のようにできます。電圧に対して遅れた電流が流れることもわかります。

  • I˙=IR˙+IL˙=V˙R−jV˙ωL=(1R−j1ωL)V˙\dot{I} = \dot{I_R} + \dot{I_L} = \frac{\dot{V}}{R} - j \frac{\dot{V}}{\omega L} = (\frac{1}{R} - j \frac{1}{\omega L})\dot{V}

また、電流の大きさ∣I∣˙\dot{|I|}は、以下のように求められます。

  • ∣I∣˙=∣V∣˙1R2+1(ωL)2\displaystyle \dot{|I|} = \dot{|V|} \sqrt{\frac{1}{R^2}+\frac{1}{(\omega L)^2}}

回路のインピーダンス

上記で導出した式と交流回路のオームの法則 Z˙=V˙I˙\dot{Z} = \frac{\dot{V}}{\dot{I}}より、この回路のインピーダンスは以下のように求められます。

  • Z˙=V˙I˙=V˙(1R−j1ωL)V˙=11R−j1ωL\displaystyle \dot{Z} = \frac{\dot{V}}{\dot{I}} = \frac{\dot{V}}{(\frac{1}{R} -j \frac{1}{\omega L})\dot{V}} = \frac{1}{\frac{1}{R} -j \frac{1}{\omega L}}

もちろん、直流回路と同様に、並列に接続されている回路素子の合成抵抗は、逆数の和として計算することもできます。なお、インピーダンスの逆数をアドミタンスと言います。交流回路の抵抗とコイル、コンダクタンスのアドミタンスをそれぞれ、コンダクタンスG=1RG=\frac{1}{R}、誘導性サセプタンスB=1ωLB = \frac{1}{\omega L}、容量性サセプタンスB=ωCB = \omega Cと呼びます。

  • 1Z˙=1ZR˙+1ZL˙=1R−j1ωL\displaystyle \frac{1}{\dot{Z}} = \frac{1}{\dot{Z_R}} + \frac{1}{\dot{Z_L}} = \frac{1}{R} - j \frac{1}{\omega L}、よって、Z˙=11R−j1ωL=jωRLR+jωL=ω2RL2R2+ω2L2+jωR2LR2+ω2L2\displaystyle \dot{Z} = \frac{1}{\frac{1}{R} - j \frac{1}{\omega L}} = \frac{j \omega R L}{R + j \omega L} = \frac{\omega^2 R L^2}{R^2 + \omega^2 L^2} + j \frac{\omega R^2 L}{R^2 + \omega^2 L^2}

また、インピーダンスの大きさ∣Z˙∣|\dot{Z}|は、以下のように求められます。

  • ∣Z∣˙=∣V∣˙∣I∣˙=∣V∣˙1R2+1(ωL)2∣V∣˙=11R2+1(ωL)2\displaystyle \dot{|Z|} = \frac{\dot{|V|}}{\dot{|I|}} = \frac{\dot{|V|}}{\sqrt{\frac{1}{R^2}+\frac{1}{(\omega L)^2}}\dot{|V|}} = \frac{1}{\sqrt{\frac{1}{R^2}+\frac{1}{(\omega L)^2}}}

ベクトル表記

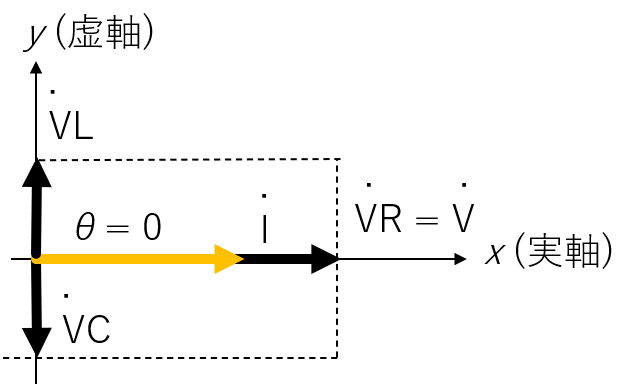
電圧を基準として、電流を静止ベクトルで表すと、下記の左の図のようになります。このとき、電流の位相は以下のように求められます。

  • θ=tan⁡−1(IL˙IR˙)=tan⁡−1(−RωL)\displaystyle \theta = \tan^{-1}(\frac{\dot{I_L}}{\dot{I_R}}) = \tan^{-1}(\frac{- R}{\omega L})

また、インピーダンスについても複素ベクトル表記ができ、下記の右の図になります。 ベクトルは第一象限にあることに注意してください。 このとき、位相差θ=tan⁡−1(RωL)\theta = \tan^{-1}(\frac{R}{\omega L})となり、位相は電流と同じですが、象限が違います。


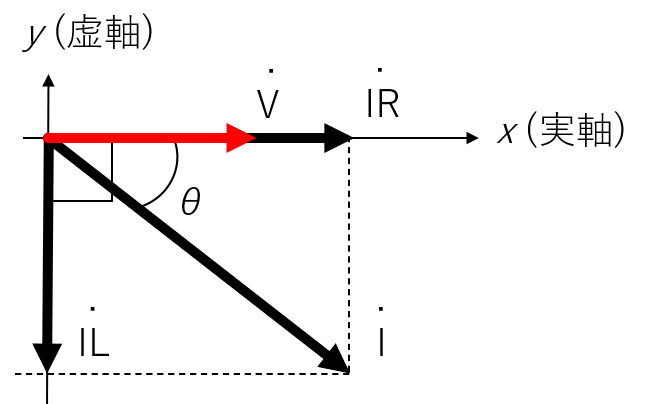
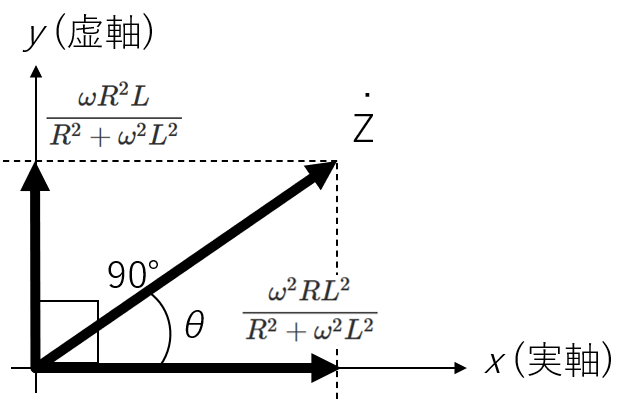
電圧と電流のベクトル表記と、インピーダンスのベクトル表記

演習問題

上記の RL 並列回路において、抵抗がRR=10[Ω\Omega]、インダクタンスがLL=20[mH]であった。この回路に実効値が 100[V]、角周波数ω\omega=500[rad/s]の交流電圧を印加した。電圧を基準としたときの、電流I˙\dot{I}を求めよ。また、複素平面上に回路のインピーダンスZ˙\dot{Z}と、電流および電圧の関係を図示せよ。

RC並列回路

以下のような、抵抗とコンデンサを正弦波交流電源に並列に接続した、RC 並列回路を考えます。また、RC並列回路のシミュレーション結果を示します。

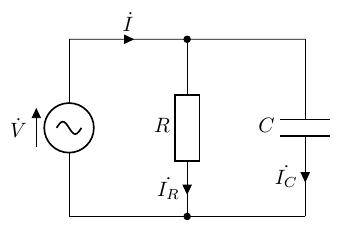
RC 並列回路も、これまでと同様の流れで解析できます。計算以外は、RL 並列回路とほぼ一緒です。

解析手順

電圧に関して

抵抗とコイルは並列に接続されているため、両者に掛かる電圧V˙\dot{V}は一緒になります。また、後述するインピーダンスZ˙\dot{Z}を用いて、電圧V˙\dot{V}と電流I˙\dot{I}の関係を表すこともでき、電流に対して遅れた電圧が印加されることもわかります。

  • V˙=I˙Z˙=1(1R+jωC)I˙\displaystyle \dot{V} = \dot{I}\dot{Z} = \frac{1}{(\frac{1}{R} + j \omega C)}\dot{I}

また、電圧の大きさ∣V˙∣|\dot{V}|は、以下のように求められます。

  • ∣V∣˙=∣I∣˙∣Z∣˙=1(1R)2+(ωC)2∣I∣˙\displaystyle \dot{|V|} = \dot{|I|}\dot{|Z|} = \frac{1}{\sqrt{(\frac{1}{R})^2 + (\omega C)^2}}\dot{|I|}

電流に関して

抵抗とコイルに流れる電流IR˙\dot{I_R}とIC˙\dot{I_C}について、キルヒホッフの電流則が成り立ちます。コンデンサのインピーダンスはXC=−j1ωCX_C = - j \frac{1}{\omega C}です。

  • 節点方程式: I˙=IR˙+IC˙\dot{I} = \dot{I_R} + \dot{I_C}
  • IR˙=V˙R\dot{I_R} = \frac{\dot{V}}{R}
  • IC˙=V˙XC=jωCV˙\dot{I_C} = \frac{\dot{V}}{X_C} = j \omega C \dot{V}

電流I˙\dot{I}を電圧V˙\dot{V}を用いて表すと以下のようにできます。電圧に対して進んだ電流が流れることもわかります。

  • I˙=IR˙+IC˙=V˙R+jωCV˙=(1R+jωC)V˙\dot{I} = \dot{I_R} + \dot{I_C} = \frac{\dot{V}}{R} + j \omega C \dot{V} = (\frac{1}{R} + j \omega C)\dot{V}

また、電流の大きさ∣I∣˙\dot{|I|}は、以下のように求められます。

  • ∣I∣˙=(1R)2+(ωC)2∣V∣˙\dot{|I|} = \sqrt{{(\frac{1}{R})^2 + (\omega C)^2}}\dot{|V|}

回路のインピーダンス

電流に関してで導出した式と交流回路のオームの法則 Z˙=V˙I˙\dot{Z} = \frac{\dot{V}}{\dot{I}}より、この回路のインピーダンスは以下のように求められます。

  • Z˙=V˙I˙=V˙(1R+jωC)V˙=11R+jωC\displaystyle \dot{Z} = \frac{\dot{V}}{\dot{I}} = \frac{\dot{V}}{(\frac{1}{R} + j \omega C)\dot{V}} = \frac{1}{\frac{1}{R} + j \omega C}

もちろん、直流回路と同様に、並列に接続されている回路素子の合成抵抗は、逆数の和として計算することもできます。

  • 1Z˙=1ZR˙+1ZC˙=1R+1−j1ωC\displaystyle \frac{1}{\dot{Z}} = \frac{1}{\dot{Z_R}} + \frac{1}{\dot{Z_C}} =\frac{1}{R} + \frac{1}{- j \frac{1}{ \omega C}}、よって、Z˙=11R+jωC=R1+jωRC=R1+ω2R2C2−jωR2C1+ω2R2C2\displaystyle \dot{Z} = \frac{1}{\frac{1}{R} + j \omega C} = \frac{R}{1 + j \omega RC} = \frac{R}{1 + \omega^2 R^2 C^2} - j \frac{\omega R^2 C}{1 + \omega^2 R^2 C^2}

また、インピーダンスの大きさ∣Z˙∣|\dot{Z}|は、以下のように求められます。

  • ∣Z∣˙=∣V∣˙∣I∣˙=∣V∣˙1R2+(ωC)2∣V∣˙=11R2+(ωC)2\displaystyle \dot{|Z|} = \frac{\dot{|V|}}{\dot{|I|}} = \frac{\dot{|V|}}{\sqrt{\frac{1}{R^2}+(\omega C)^2}\dot{|V|}} = \frac{1}{\sqrt{\frac{1}{R^2}+(\omega C)^2}}

ベクトル表記

電圧を基準として、電流を静止ベクトルで表すと、下記の左の図のようになります。このとき、電流の位相は以下のように求められます。

  • θ=tan⁡−1(IC˙IR˙)=tan⁡−1(ωCR)\displaystyle \theta = \tan^{-1}(\frac{\dot{I_C}}{\dot{I_R}}) = \tan^{-1}(\omega C R)

また、インピーダンスについても複素ベクトル表記ができ、ベクトルは第二象限にあることに注意してください。 このとき、位相差θ=tan⁡−1(ωCR)\theta = \tan^{-1}(\omega C R)となり、位相は電流と同じですが、象限が違います。


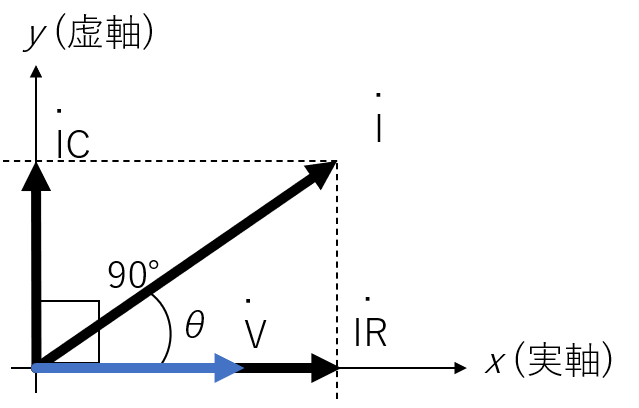
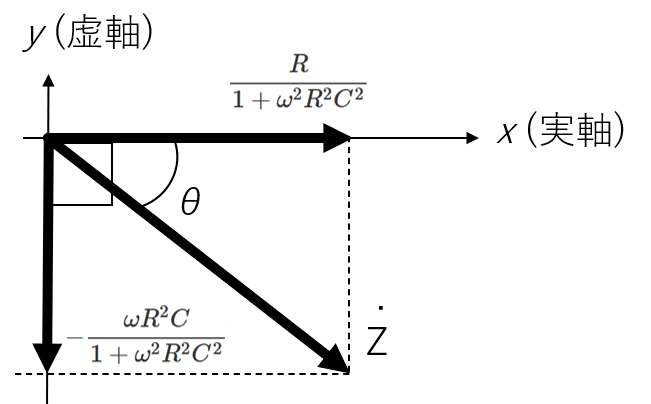
電圧と電流のベクトル表記と、インピーダンスのベクトル表記

演習問題

上記の RC 並列回路において、抵抗がRR=5[Ω\Omega]、キャパシタンスがCC=200[μ\muF]であった。この回路に実効値が 100[V]、角周波数ω\omega=500[rad/s]の交流電圧を印加した。電圧を基準としたときの、電流I˙\dot{I}を求めよ。また、複素平面上に回路のインピーダンスZ˙\dot{Z}と、電流および電圧の関係を図示せよ。

RLC並列回路

以下のような、抵抗とコイルとコンデンサを正弦波交流電源に直列に接続した、RLC 並列回路を考えます。また、RLC並列回路のシミュレーション結果を示します。

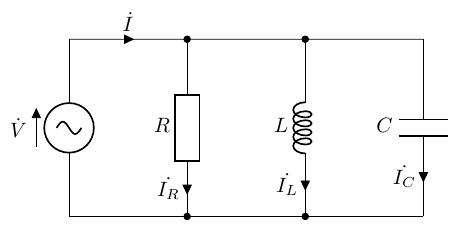
RLC 並列回路は挙動が複雑ですが、解析自体は RL 並列回路や RC 並列回路と同様に解析できます。

解析手順

電圧に関して

抵抗とコイル、コンデンサは並列に接続されているため、各回路素子に掛かる電圧V˙\dot{V}は一緒になります。また、後述するインピーダンスZ˙\dot{Z}を用いて、電圧V˙\dot{V}と電流I˙\dot{I}の関係を表すこともできます。電流と電圧の位相の関係は、コイルとコンデンサのインピーダンスの大小によって決まる、と言えます。

  • V˙=I˙Z˙=1(1R+j(−1ωL+ωC))I˙\displaystyle \dot{V} = \dot{I}\dot{Z} = \frac{1}{(\frac{1}{R} + j (- \frac{1}{\omega L} + \omega C))}\dot{I}

また、電圧の大きさ∣V˙∣|\dot{V}|は、以下のように求められます。

  • ∣V∣˙=∣I∣˙∣Z∣˙=11R2+(−1ωL+ωC)2∣I∣˙\displaystyle \dot{|V|} = \dot{|I|}\dot{|Z|} = \frac{1}{\sqrt{\frac{1}{R^2} + (- \frac{1}{\omega L} + \omega C)^2}}\dot{|I|}

電流に関して

抵抗とコイル、コンデンサに流れる電流IR˙\dot{I_R}とIL˙\dot{I_L}、IC˙\dot{I_C}について、キルヒホッフの電流則が成り立ちます。

  • 節点方程式: I˙=IR˙+IL˙+IC˙\dot{I} = \dot{I_R} + \dot{I_L} + \dot{I_C}
  • IR˙=V˙R\dot{I_R} = \frac{\dot{V}}{R}
  • IL˙=−j1ωLV˙\dot{I_L} = - j \frac{1}{\omega L} \dot{V}
  • IC˙=V˙XC=jωCV˙\dot{I_C} = \frac{\dot{V}}{X_C} = j \omega C \dot{V}

電流I˙\dot{I}を電圧V˙\dot{V}を用いて表すと以下のようにできます。

  • I˙=IR˙+IL˙+IC˙=V˙R−j1ωLV˙+jωCV˙=(1R+j(−1ωL+ωC))V˙\dot{I} = \dot{I_R} + \dot{I_L} + \dot{I_C} = \frac{\dot{V}}{R} - j \frac{1}{\omega L} \dot{V} + j \omega C \dot{V} = (\frac{1}{R} + j (- \frac{1}{\omega L} + \omega C)) \dot{V}

また、電流の大きさ∣I˙∣|\dot{I}|は、以下のように求められます。

  • ∣I˙∣=1R2+(−1ωL+ωC)2∣V∣˙|\dot{I}| = \sqrt{\frac{1}{R^2} + (- \frac{1}{\omega L} + \omega C)^2} \dot{|V|}

回路のインピーダンス

電流に関してで導出した式と交流回路のオームの法則 Z˙=V˙I˙\dot{Z} = \frac{\dot{V}}{\dot{I}}より、この回路のインピーダンスは以下のように求められます。

  • Z˙=V˙I˙=V˙(1R+j(−1ωL+ωC))V˙=1(1R+j(−1ωL+ωC))\displaystyle \dot{Z} = \frac{\dot{V}}{\dot{I}} = \frac{\dot{V}}{(\frac{1}{R} + j (- \frac{1}{\omega L} + \omega C)) \dot{V}} = \frac{1}{(\frac{1}{R} + j (- \frac{1}{\omega L} + \omega C))}

もちろん、直流回路と同様に、並列に接続されている回路素子の合成抵抗は、逆数の和として計算することもできます。このくらいになってくると、インピーダンスの逆数のアドミタンスを使ったほうがよいかもしれません。

  • 1Z˙=1ZR˙+1ZC˙+1ZL˙=1R+1−j1ωC+1jωL\displaystyle \frac{1}{\dot{Z}} = \frac{1}{\dot{Z_R}} + \frac{1}{\dot{Z_C}} + \frac{1}{\dot{Z_L}} =\frac{1}{R} + \frac{1}{- j \frac{1}{\omega C}} + {\frac{1}{j \omega L}}、よって、Z˙=11R+j(−1ωL+ωC)\displaystyle \dot{Z} = \frac{1}{\frac{1}{R} + j (- \frac{1}{\omega L} + \omega C)}

また、インピーダンスの大きさ∣Z˙∣|\dot{Z}|は、以下のように求められます。

  • ∣Z∣˙=∣V∣˙∣I∣˙=∣V∣˙1R2+(−1ωL+ωC)2∣V∣˙=11R2+(−1ωL+ωC)2\displaystyle \dot{|Z|} = \frac{\dot{|V|}}{\dot{|I|}} = \frac{\dot{|V|}}{\sqrt{\frac{1}{R^2}+ (- \frac{1}{\omega L} + \omega C)^2}\dot{|V|}} = \frac{1}{\sqrt{\frac{1}{R^2}+(- \frac{1}{\omega L} + \omega C)^2}}

ベクトル表記

電圧を基準として、電流を静止ベクトルで表すと、下記の左の図のようになります。このとき、電流の位相は以下のように求められます。

  • θ=tan⁡−1(IC˙−IL˙IR˙)=tan⁡−1((ωC−1ωL)R)\displaystyle \theta = \tan^{-1}(\frac{\dot{I_C} - \dot{I_L}}{\dot{I_R}}) = \tan^{-1}((\omega C - \frac{1}{\omega L})R)

また、インピーダンスについても複素ベクトル表記ができ、下記の右の図になります。 このとき、位相差θ=tan⁡−1((ωC−1ωL)R)\theta = \tan^{-1}((\omega C - \frac{1}{\omega L})R)となり、電流の位相差と同じことがわかります。


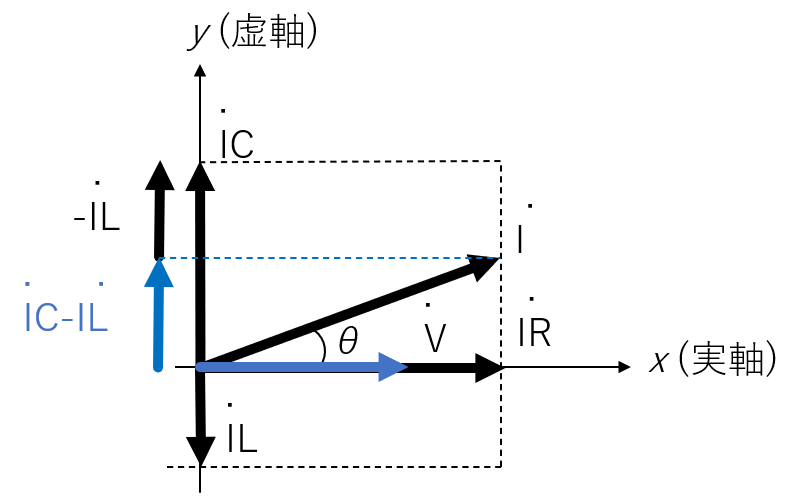
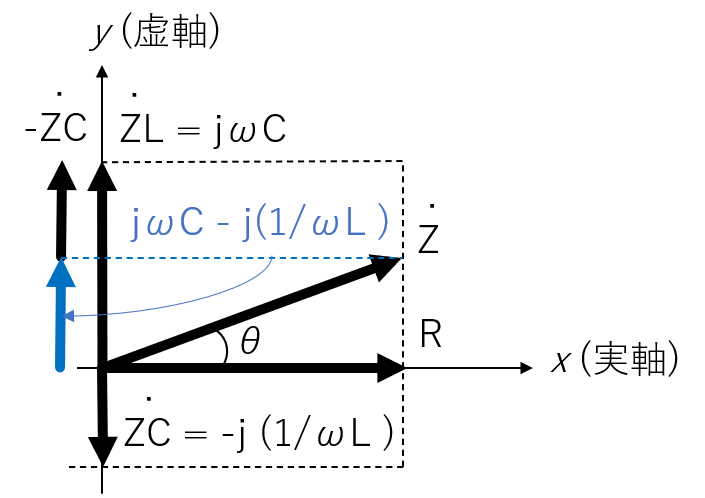
電圧と電流のベクトル表記と、インピーダンスのベクトル表記

その他

RLC 直流回路と同様に、RLC 並列回路も共振状態を取ります。考え方は直列回路と一緒で、電流I˙\dot{I}の位相は、コイルのリアクタンスXLX_LとコンデンサのリアクタンスXCX_Cの大小関係で変化します。つまり、この 2 つのリアクタンスの大きさが一緒のとき、XL−XC=0X_L - X_C = 0となり、リアクタンス成分は最小の零になります。その結果、電流の位相も零となり、インピーダンスは抵抗だけとなります。このときこの回路に流れる電流の大きさが最大となり、この状態を共振と呼びます。

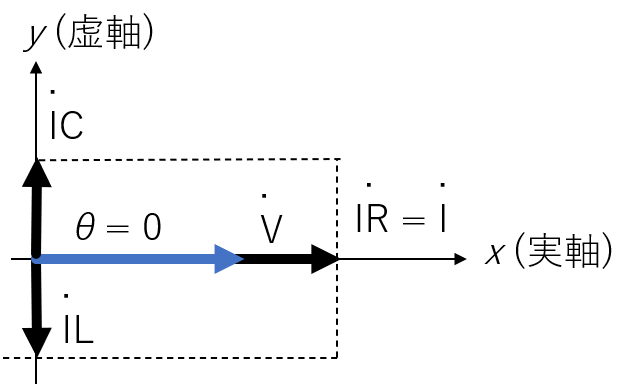
以下に、交流電圧源の周波数を 41.1Hz とし、コイルのリアクタンスXLX_LとコンデンサのリアクタンスXCX_Cを変化させたときの RLC 直列回路のシミュレーション結果を示します。XLX_L = 1[H], XCX_C = 15[μ\muF]のときに共振状態となり、回路に流れる電流が最大となります。

共振しているRLC並列回路

演習問題

参考書 1 の P.93 例題 7.4
上記の RLC 並列回路において、抵抗がRR=5[Ω\Omega]、インダクタンスがLL=40[mH]、キャパシタンスCC=200[μ\muF]であった。この回路に瞬時値がv=1002sin⁡500tv = 100 \sqrt{2}\sin500tで与えられる電圧を加える。
(1) この回路の合成アドミタンスを求めよ。
(2) 各素子に流れる電流を求めよ。