コンテンツにスキップ

第11回 基本素子の交流回路

ここでは、交流回路につながれた基本素子、すなわち、抵抗、コイル、コンデンサを取り扱います。 具体的には、それぞれのしくみを簡単に説明し、交流電圧源と抵抗/コイル/コンデンサがつながれた回路の挙動を解析します。 また、解析には前回学んだ複素ベクトル表記などを利用します。 交流回路の解析にも直流回路で学んだオームの法則やキルヒホッフの法則などが利用できるので、その点では大丈夫です。 しかし、交流回路に特有の位相やインピーダンスと言った要素が回路の解析を複雑にしていますので、注意してください。

なお、今回の講義資料は、本講義の参考書 1 の「第 6 章基本素子の交流回路」と、教科書の第 7 章 7.2 節、7.4 節、8.3.2 節をもとに作成されています。

今回出てくる回路のシミュレーション結果はここにまとめています。 また、今回出てくる交流電圧源の式は、以下のとおりとします。

  • 三角関数表記: v=Vmsin⁡(ωt)=2Vesin⁡(ωt)v = V_m \sin(\omega t) = \sqrt{2} V_{e} \sin (\omega t)
  • 複素ベクトル表記: V˙=Ve\dot{V} = V_{e}

抵抗と交流回路

抵抗は交流回路でも直流回路とまったく同じに扱うことができますので、原理の説明などはせずに、抵抗のみを持つ簡単な回路を解析してみます。

抵抗のみを持つ回路

以下のように、交流電圧源vvに抵抗RRのみを接続した回路を考えます。 シミュレーション結果は左端の回路になります。

三角関数による回路解析

交流回路にもオームの法則は適用できるので、RRに流れる電流iiは、以下のように計算できます。

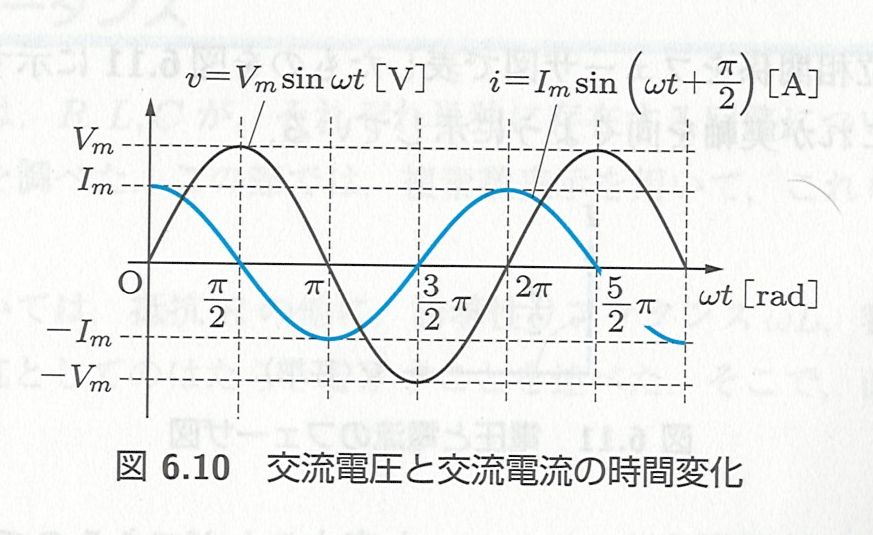
i=vR=VmRsin⁡(ωt)=Imsin⁡(ωt)i = \frac{v}{R} = \frac{V_m}{R} \sin(\omega t) = I_m \sin(\omega t)

交流電圧源v=Vmsin⁡(ωt)v = V_m \sin(\omega t)と比べると、抵抗に流れる電流は、電圧と同じ位相で変化する（同相）と言えます。

複素ベクトル表記

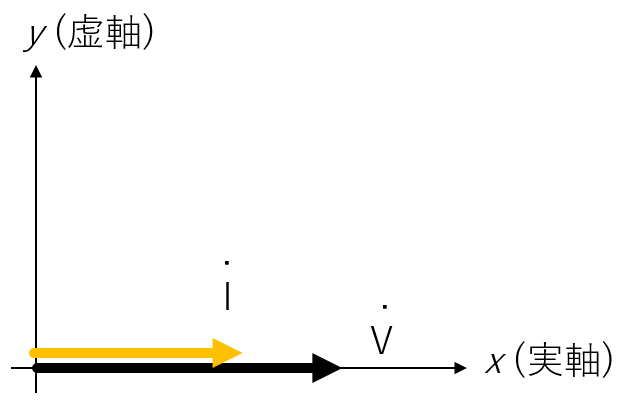
静止ベクトルで表すと、以下のようになります。

  • 電流と電圧の関係（電圧基準）: I˙=V˙R\dot{I} = \frac{\dot{V}}{R}
  • 電圧と電流の関係（電流基準）: V˙=RI˙\dot{V} = R \dot{I}
  • 静止ベクトルの図

まとめ

  • 電圧を基準にすると、電流iiは、電圧vvの位相と一緒。つまり、I˙=V˙R\dot{I} = \frac{\dot{V}}{R}
  • 電流を基準にすると、電圧vvは、電流iiの位相と一緒。つまり、V˙=RI˙\dot{V} = R \dot{I}
  • 抵抗RR[Ω\Omega]は、直流と同様に電流に対する抵抗の具合を示す。

演習問題

上の図の回路で、抵抗RR=20[Ω\Omega]で、交流電圧v=1002sin⁡(ωt)v=100\sqrt{2}\sin(\omega t)[V]のとき、回路に流れる電流iiの大きさ（実効値）を求めよ。

コンデンサと交流回路

ここでは、コンデンサのしくみを簡単に説明し、交流電圧源とコンデンサのみを持つ簡単な回路を解析してみます。

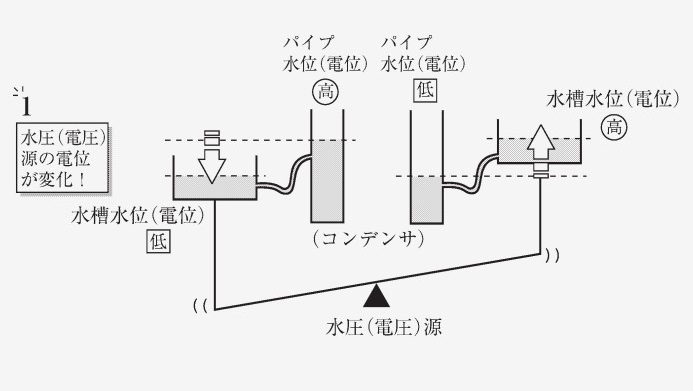
コンデンサのしくみ

コンデンサは、2 枚の平板を並べたもので、電気回路の分野ではキャパシタとも呼ばれます。 応用先としては、交流電流を直流電流に変換するコンバータ（平滑回路）が挙げられます。参考サイト1には、これらのしくみが詳しく述べられています。 以下に、一般的なコンデンサの形状と回路記号を示します。

出典: 日本ケミコン株式会社の企業情報・インターンシップ | キャリタス就活2023

回路におけるコンデンサの動作は、言葉で説明するよりシミュレーション結果の右端の回路を見たほうが分かりやすいと思います。 交流電圧源の電圧から見ると電流の位相がずれている（π2\frac{\pi}{2}進んでいる）ことがわかるかと思います。

詳しくは電気磁気学で取り扱う内容ですが、動作を言葉で説明すると次のようになります。まず、コンデンサに電流が流れると、電荷が流入し始めます。コンデンサの容量の上限まで電荷が貯まると、それ以上は電荷の変化がなくなり、電流は流れなくなります。次に、交流電圧源の電位が切り替わり、電流が逆方向に流れると、貯まった電荷は流出し始めます。コンデンサに電荷が流入・流出することが、あたかもコンデンサに電流が流れているかのように見える、というわけです。なお、直流電流では、電流が一方向にしか移動せず、コンデンサに電荷がたまり続け、最終的にコンデンサに電流は流れなくなります。

教科書の P.129 ではこの動作が図を使って示されています。

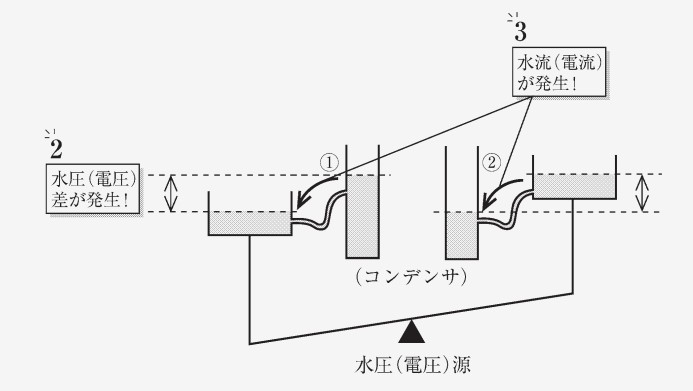
コンデンサに流れる電流は以下のように表されます。なお、CCをコンデンサの容量（キャパシタンス）とします。

  • コンデンサに流れる電流 ic=Cdvdti_c = C \frac{dv}{dt}

コンデンサのみを持つ回路

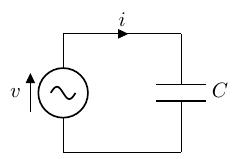
以下のように、交流電圧源vvにコンデンサCCのみを接続した回路を考えます。 この回路のシミュレーション結果（再掲）は、ここの右端の回路です。 なお、シミュレータでは、抵抗を入れないとシミュレーションできないため、便宜的に抵抗を入れています。

三角関数による回路解析

ここで、電圧v=Vmsin⁡(ωt)v = V_m \sin (\omega t)を印加すると、コンデンサCCに流れる電流iCi_Cは、以下のように計算できます。

iC=Cdvdt=ωCVmcos⁡(ωt)=ωCVmsin⁡(ωt+π2)i_C = C \frac{dv}{dt} = \omega C V_m \cos(\omega t) = \omega C V_m \sin(\omega t + \frac{\pi}{2})[A]

これをオームの法則(i=vRi = \frac{v}{R})と比較すると、以下のように対応していることがわかります。

  • 抵抗 R⇔1ωCR \Leftrightarrow \frac{1}{\omega C}
  • コンデンサに掛かる電圧 vc⇔Vmsin⁡(ωt+π2)v_c \Leftrightarrow V_m \sin (\omega t + \frac{\pi}{2})

つまり、抵抗値 1ωC\frac{1}{\omega C}[Ω\Omega]を持ち、電圧から見ると電流の位相をπ2\frac{\pi}{2}だけ進める作用を持つ抵抗成分と言えることになります。 逆に、電流から見ると電圧の位相をπ2\frac{\pi}{2}だけ遅らせる作用を持つ抵抗成分と言えます。 また、1ωC\frac{1}{\omega C}の部分を容量性リアクタンスXC[ΩX_C [\Omega]と呼び、交流に対する抵抗としての働きを示します。

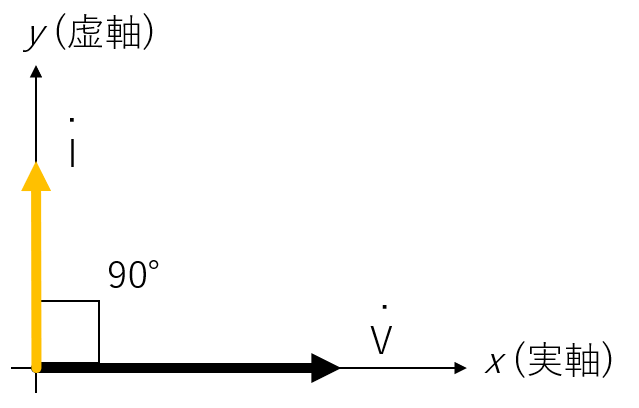
複素ベクトル表記

静止ベクトルで表すと、以下のようになります。前回学んだ様に、jjには位相をπ2\frac{\pi}{2}[rad]進ませる回転オペレータとしての機能があります。

  • 電流と電圧の関係（電圧基準）: I˙=jωCV˙\dot{I} = j \omega C \dot{V}
  • 電圧と電流の関係（電流基準）: V˙=−j1ωCI˙\dot{V} = -j \frac{1}{\omega C} \dot{I}
  • 静止ベクトルの図

まとめ

  • 電圧を基準にすると、電流iiは、電圧vvの位相よりπ2\frac{\pi}{2}進んでいる。つまり、I˙=jωCV˙\dot{I} = j \omega C \dot{V}
  • 電流を基準にすると、電圧vvは、電流iiの位相よりπ2\frac{\pi}{2}遅れている。つまり、V˙=−j1ωCI˙\dot{V} = -j \frac{1}{\omega C} \dot{I}
  • 容量性リアクタンス 1ωC\frac{1}{\omega C}[Ω\Omega]は、交流におけるコンデンサCCの抵抗の具合を示す
  • コンデンサの電圧と電流の関係（参考書 1 P.73, 図中ではIm=ωCVmI_m = \omega C V_m）

演習問題

参考書 1 の P.75 例題 6.3
上記のコンデンサと交流電圧のみを接続した回路において、C=20[μF]C=20[\mu F]のキャパシタンスをもつコンデンサに交流電圧V˙=250∠(−30∘)\dot{V} = 250 \angle (-30^{\circ}) (v=1253−125jv = 125\sqrt{3} - 125 j) [V]を加えた。周波数ffを 50[Hz]とする。容量性リアクタンスXCX_Cを求めよ。また、この回路に流れる電流をフェーザ形式で求め、フェーザ図(静止ベクトル)を描け。

コイルと交流回路

ここでは、コンデンサのしくみを簡単に説明し、交流電圧源とコンデンサのみを持つ簡単な回路を解析してみます。

コイルのしくみ

コイルは、電線を螺旋状に巻いたもので、電気回路の分野ではインダクタンスとも呼ばれます。 応用先としては、交流電流を別の交流電流に変換するトランスフォーマが挙げられます。 以下に、一般的なコイル（チョークコイル）の形状と回路記号を示します。

出典: 日立金属＞製品情報＞ファインメット®＞コモンモードチョーク＞コイル

回路におけるコイルの動作も、言葉で説明するよりシミュレーション結果の真ん中の回路を見たほうが分かりやすいと思います。 交流電圧源の電圧から見ると電流の位相がずれている（π2\frac{\pi}{2}遅れている）ことがわかるかと思います。

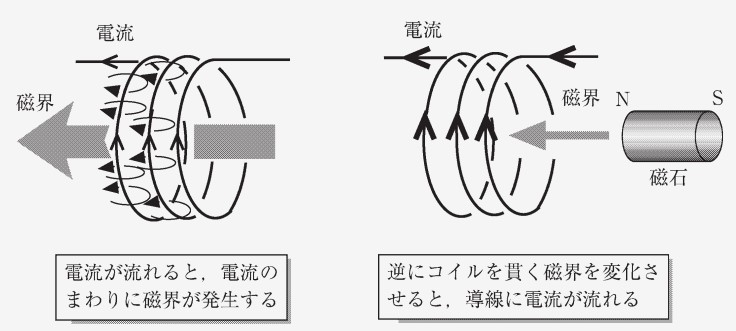
詳しくは電気磁気学で取り扱う内容ですが、動作を言葉で説明すると次のようになります。まず、電線やコイルに電流が流れると、その部分に発生する磁束Φ\Phiも変化し、起電力が発生します。 起電力の方向と大きさは、ファラデーの電磁誘導の法則から以下のとおりとなります。この法則を利用して、コイルは電流の安定化や電圧変換などに利用されています。

  1. 方向は、磁束の変化を妨げる向きと同じ（ファラデーの電磁誘導の法則第 1 法則）
  2. 大きさは、磁束の時間変化の大きさに比例（ファラデーの電磁誘導の法則第 2 法則）

教科書の P.131 ではこの動作が図を使って示されています。

コイルで発生する起電力e0e_0は、以下のように電流iiを時間ttで偏微分した形で表されます。 式の意味は、電流の時間変化の度合いに自己インダクタンスLLを掛けたものが起電力になる、というものです。 また、マイナスの符号は、ファラデーの電磁誘導の法則から導かれた電流の方向を示すものです。 なお、LLを自己インダクタンスと言い、起電力の発生させ具合を示します。

  • コイルの起電力 e0=−Ldidte_0 = - L \frac{di}{dt}[V]

回路においては、印加された電圧vvと発生した起電力e0e_0がお互いに釣り合っているので、v+e0=0v + e_0 = 0となり、電圧を起電力を使って表すことができます。

  • コイルに印加された電圧 v=−e0=Ldidtv = - e_0 = L \frac{di}{dt}[V]

コイルのみを持つ回路

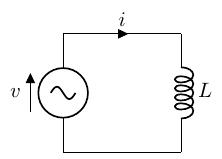
以下のように、交流電圧源vvにコイルLLのみを接続した回路を考えます。 この回路のシミュレーション結果（再掲）は、ここの真ん中の回路です。 なお、シミュレータでは、コンデンサと条件を一致させるために便宜的に抵抗を入れています。

三角関数による回路解析

ここで、電圧v=Vmsin⁡(ωt)v = V_m \sin (\omega t)を印加すると、コイルLLに流れる電流iLi_Lは、以下のように計算できます。

iL=1L∫vdt=1L∫Vmsin⁡(ωt)dt=−VmωLcos⁡(ωt)=1ωLVmsin⁡(ωt−π2)i_L = \frac{1}{L} \int v dt = \frac{1}{L} \int V_m \sin(\omega t) dt = -\frac{V_m}{\omega L} \cos(\omega t) = \frac{1}{\omega L} V_m \sin(\omega t - \frac{\pi}{2})

これをオームの法則(i=vRi = \frac{v}{R})と比較すると、以下のように対応していることがわかります。

  • 抵抗 R⇔ωLR \Leftrightarrow \omega L
  • コイルに掛かる電圧 vc⇔Vmsin⁡(ωt−π2)v_c \Leftrightarrow V_m \sin (\omega t - \frac{\pi}{2})

つまり、抵抗値 ωL\omega L[Ω\Omega]を持ち、電圧から見ると電流の位相をπ2\frac{\pi}{2}だけ遅らせる作用を持つ抵抗成分と言えることになります。 逆に、電流から見ると電圧の位相をπ2\frac{\pi}{2}だけ進める作用を持つ抵抗成分と言えます。 また、ωL\omega Lの部分を誘導性リアクタンスXL[ΩX_L [\Omega]と呼び、交流に対する抵抗としての働きを示します。

複素ベクトル表記

静止ベクトルで表すと、以下のようになります。 前回学んだ様に、j には位相をπ2\frac{\pi}{2}[rad]進ませる回転オペレータとしての機能があります。

  • 電流と電圧の関係（電圧基準）: I˙=−j1ωLV˙\dot{I} = -j \frac{1}{\omega L} \dot{V}
  • 電圧と電流の関係（電流基準）: V˙=jωLI˙\dot{V} = j \omega L \dot{I}
  • 静止ベクトルの図

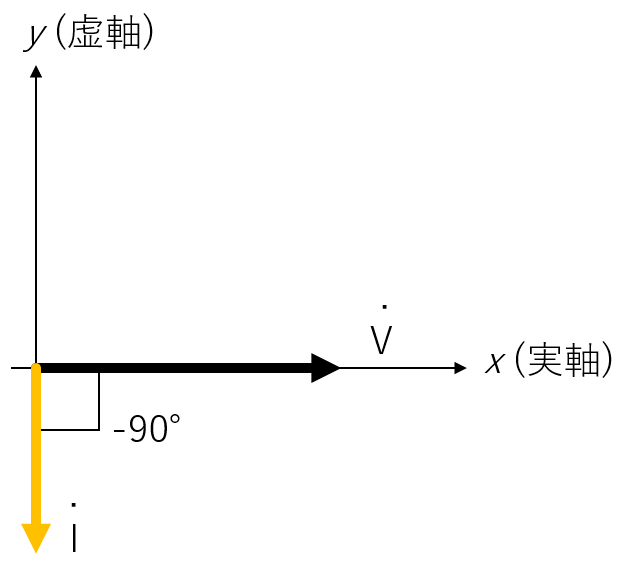
まとめ

  • 電圧を基準にすると、電流iiは、電圧vvの位相よりπ2\frac{\pi}{2}遅れている。つまり、I˙=−j1ωLV˙\dot{I} = -j \frac{1}{\omega L} \dot{V}
  • 電流を基準にすると、電圧vvは、電流iiの位相よりπ2\frac{\pi}{2}進んでいる。つまり、V˙=jωLI˙\dot{V} = j \omega L \dot{I}
  • 誘導性リアクタンス ωL\omega L[Ω\Omega]は、交流におけるコイルLLの抵抗の具合を示す
  • コイルの電圧と電流の関係（参考書 1 P.70, 図中ではIm=VmωLI_m = \frac{V_m}{\omega L}）

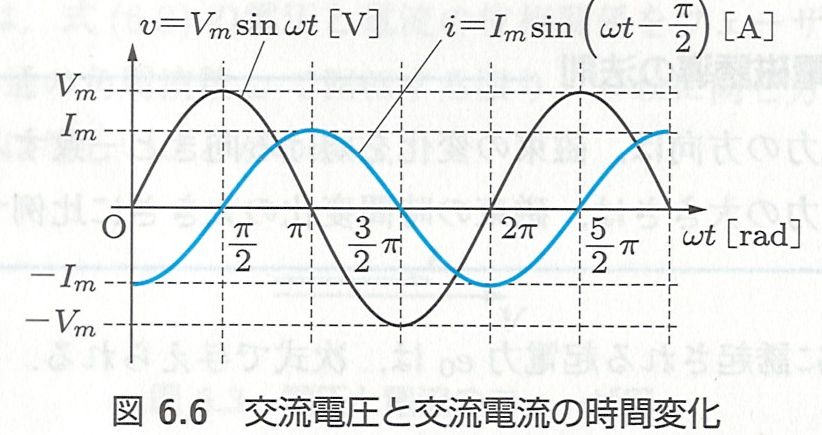
演習問題

参考書 1 の P.72 例題 6.2
上記のコイルと交流電圧のみを接続した回路において、LL = 200[mH]のインダクタンスをもつコイルに交流電圧 V˙=250∠(−30∘)\dot{V} = 250 \angle (-30^{\circ}) (v=1253−125jv = 125\sqrt{3} - 125 j) [V]を加えた。周波数ffを 50[Hz]とする。誘導性リアクタンスXLX_Lを求めよ。また、この回路に流れる電流をフェーザ形式で求め、フェーザ図(静止ベクトル)を描け。

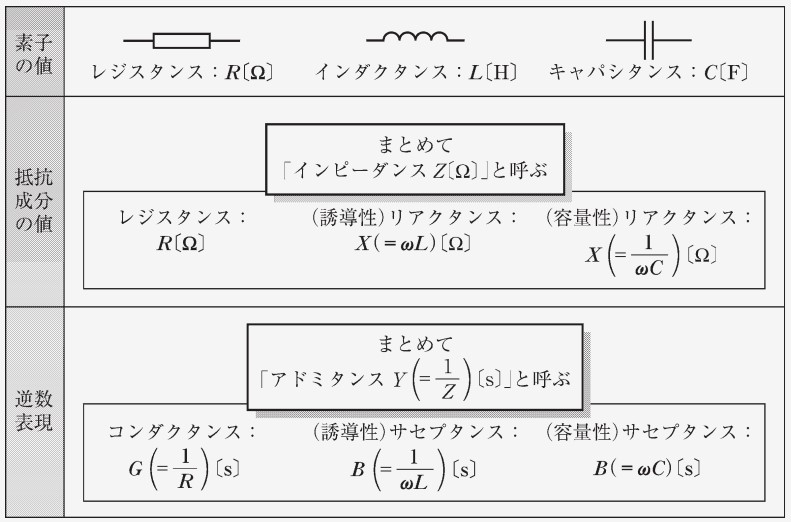
抵抗、コイル、コンデンサのまとめ

今回扱った、抵抗、コイル、コンデンサの電流の複素ベクトル表記と電圧V˙\dot{V}に対する位相差を以下にまとめます。

回路素子 電圧V˙\dot{V} 電流I˙\dot{I} I˙\dot{I}とV˙\dot{V}の位相差 インピーダンスZ˙\dot{Z}
抵抗 RR V˙=RI˙\dot{V} = R\dot{I} I˙=V˙R\dot{I} = \frac{\dot{V}}{R} 同相 レジスタンス RR
コイル LL V˙=jωLI˙\dot{V} = j \omega L \dot{I} I˙=−j1ωLV˙\dot{I} = -j \frac{1}{\omega L} \dot{V} 電流がπ2\frac{\pi}{2}遅れる 誘導性リアクタンス jωLj {\omega L}
コンデンサ CC V˙=−j1ωCI˙\dot{V} = -j \frac{1}{\omega C}\dot{I} I˙=jωCV˙\dot{I} = j \omega C \dot{V} 電流がπ2\frac{\pi}{2}進む 容量性リアクタンス −j1ωC-j \frac{1}{\omega C}

教科書の P.173 では、以下のように三角関数での回路解析と複素ベクトル表記の対応関係がまとめられています。

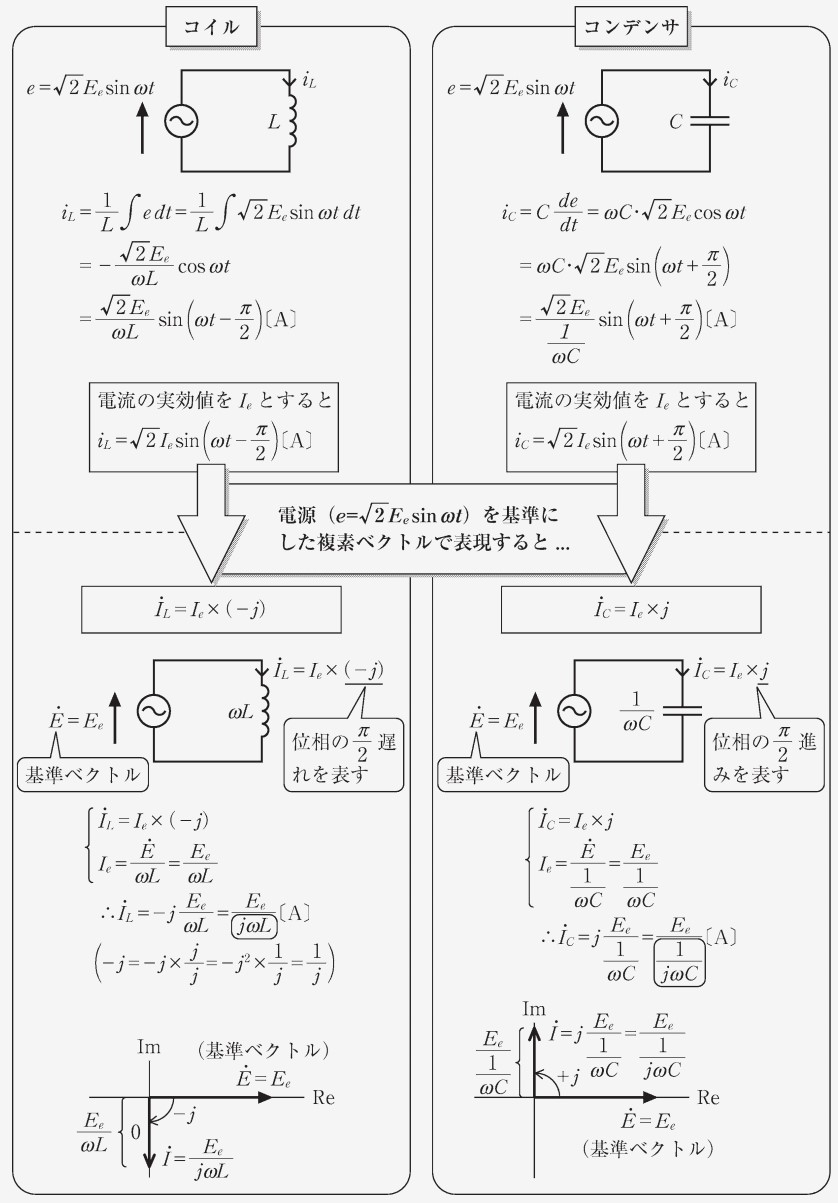
インピーダンス

ここまで見てきた様に、交流回路のコイルとコンデンサには、オームの法則の抵抗に相当するリアクタンスと言うものがありました。 ここでは、オームの法則の観点からこれらを擬似的な抵抗成分としてまとめて扱うインピーダンスという考え方について述べます。

  • コイルの擬似的な抵抗成分 = 誘導性リアクタンス = ωL\omega L
  • コンデンサの擬似的な抵抗成分 = 容量性リアクタンス = 1ωC\frac{1}{\omega C}

直流回路のオームの法則はV=IRV = IRでしたが、交流回路では抵抗RRの部分に純粋な抵抗のほかにリアクタンスが入ることになります。 ですので、交流回路では抵抗に相当する部分をインピーダンスZ˙\dot{Z}というものに拡張します。 また、インピーダンスの逆数をアドミタンスと呼びます。 インピーダンスを用いると、交流回路のオームの法則は以下のように表せます。

  • 交流回路のオームの法則: V˙=Z˙I˙\dot{V} = \dot{Z} \dot{I}、もしくは、Z˙=V˙I˙\dot{Z} = \frac{\dot{V}}{\dot{I}}

※あまり明確になっていない思うのですが、インピーダンスやアドミタンスと言った場合は、複素ベクトル（つまり、jjが入る）に言及していることが大多数です。また、レジスタンスやリアクタンスと言った場合は、その大きさのみ（つまり、jjが入らない）に言及していることが多いです。これは、インピーダンスやアドミタンスは、レジスタンスやリアクタンスを合成したものとして言及されるからです。

コンデンサと交流回路やコイルと交流回路で見てきた、交流電圧源にコイルやコンデンサのみがつながれた回路で、それぞれのインピーダンスの式とその値を変化させたときのシミュレーション結果を以下に示します。

抵抗のみの回路

コイルのみの回路

コンデンサのみの回路

教科書の P.140 に抵抗/コイル/コンデンサ、インピーダンス、アドミタンスの関係がまとめてあります。

  1. コンデンサの基礎知識とハイブリッドコンデンサ - 電子デバイス・産業用機器 - Panasonic ↩