コンテンツにスキップ

第13回 交流の電力

ここでは、交流回路の電力について取り扱います。 交流回路では電力も時間に沿って変化、それに伴う交流ならではの考え方が出てきます。 そのため、直流回路の電力と異なり、三種類の電力（有効電力、無効電力、皮相電力）が出てきます。 ポイントは、実際に電力を消費するのは抵抗のみで、コイルやコンデンサは電力を出し入れしているだけ、ということです。

今回の講義資料は、主に参考書 1 の「第 8 章交流の電力」をもとに作成されています。 本講義の教科書の第 7 章 7.3 節と 8.4 節にも同様のことが説明されており、補足的な資料として使っています。 なお、教科書では位相にはϕ\phiが使われていますが、本講義資料では参考書に合わせてθ\thetaを使っています。

交流の電力のイメージ

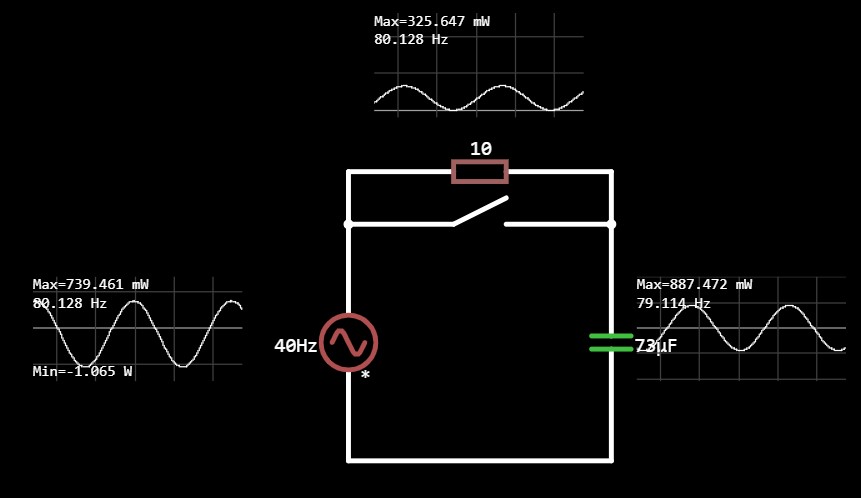
まず初めに、 交流のRC直列回路の瞬時電力のシミュレーション結果 を用いて、交流回路の電力がどういうものかをイメージします。 ポイントは、以下のとおりです。

  1. 交流電力源が、全体の電力を供給している（＝ 瞬時電力と皮相電力）
  2. 抵抗のみが、実際の電力を消費している（＝ 有効電力）
  3. コイルやコンデンサは、電力を出し入れしているだけ（＝ 無効電力）

三角関数を用いた解析

ここからは、三角関数を用いて電力の計算を行い、交流回路の電力がどういうものかを理解します。 以下のように交流回路のインピーダンスをzzとしてひとまとめにした回路を考えます。

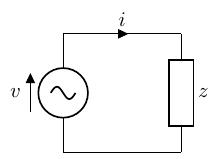
この回路に、以下の瞬時電流iiが流れ、瞬時電圧vvが印加されているとします。 コイルやコンデンサによって、電流の位相はθ\thetaだけ電圧に対して遅れている形です。

  • 瞬時電圧 v=2Vesin⁡(ωt)v = \sqrt{2} V_{e} \sin (\omega t)
  • 瞬時電流 i=2Iesin⁡(ωt−θ)i = \sqrt{2} I_{e} \sin (\omega t - \theta)

瞬時電力

第2回 電力と電力量で取り扱った様に、直流回路の電力はP=IV=I2R=V2RP = IV = I^2 R = \frac{V^2}{R}で求めることができます。 交流回路についても同様ですので、振幅に対応できるように各値を三角関数を用いた瞬時値の形に直し、これを瞬時電力ppと言います。細かい話ですが、電力とは大きさを示すものです。

  • 瞬時電力 p=iv=i2z=v2zp = i v = i^2 z = \frac{v^2}{z}

瞬時電力の式に、瞬時電圧と瞬時電流を代入すると以下のように解けます。

  • 瞬時電力 p=iv=2Vesin⁡(ωt)⋅2Iesin⁡(ωt−θ)=2VeIe(sin⁡(ωt)sin⁡(ωt−θ))=2VeIe(−12)(cos⁡(2ωt−θ)−cos⁡θ)=VeIe(cos⁡θ−cos⁡(2ωt−θ))\displaystyle p = i v = \sqrt{2} V_{e} \sin (\omega t) \cdot \sqrt{2} I_{e} \sin (\omega t - \theta) = 2 V_{e} I_{e} (\sin (\omega t) \sin(\omega t - \theta)) = 2 V_{e} I_{e} (-\frac{1}{2}) (\cos(2 \omega t - \theta) - \cos \theta) = V_{e} I_{e} (\cos\theta - \cos(2 \omega t - \theta))

瞬時電力の意味

瞬時電力は、これ以降で説明する有効電力や無効電力と異なり、「ある瞬間で発生する」という意味は、第 2 項で表される電力は、コイルやコンデンサを往復するだけで、1 周期のタイムスパンでは消費されない、ということです。

有効電力

瞬時電力ppの 1 周期についての平均値PeP_eを求めてみます。つまり、ppを 1 周期分（ωt=\omega t = 0 ～ 2π2 \pi）だけ積分し、それを 1 周期（2π2 \pi）で割ります。表記を簡単にするために、ωt=ϕ\omega t = \phiとします。

  • Pe=12π∫02πpdϕ=12π∫02π(VeIecos⁡θ−VeIecos⁡(2ϕ−θ))dϕ=VeIe2π([ϕcos⁡θ]02π−12[sin⁡(2ϕ−θ)]02π)=VeIe2π(2πcos⁡θ)=VeIecos⁡θ\displaystyle P_e = \frac{1}{2 \pi} \int^{2 \pi}_{0} p d \phi = \frac{1}{2 \pi} \int^{2 \pi}_{0} \left(V_{e} I_{e} \cos\theta - V_{e} I_{e} \cos(2 \phi - \theta) \right) d \phi = \frac{V_{e} I_{e}}{2 \pi} \left([\phi \cos \theta]^{2 \pi}_{0} - \frac{1}{2}[\sin (2 \phi - \theta)]^{2 \pi}_{0} \right) = \frac{V_{e} I_{e}}{2 \pi}(2 \pi \cos \theta) = V_{e} I_{e} \cos \theta

つまり、瞬時電力ppの第 1 項の定数項のみが残ったものが実際に消費される電力PeP_eとなり、これを有効電力 (Effective power) と言います。言い換えると、有効電力PeP_eは、電圧の実効値VeV_eと電流の実効値IeI_eの積と、両者の位相差θ\thetaで決まるcos⁡θ\cos \thetaを掛けた値です。有効電力の単位は[W]（ワット, watt）です。細かい話ですが、電力とは大きさを示すものです。

  • 有効電力 Pe=VeIecos⁡θ\displaystyle P_e = V_{e} I_{e} \cos \theta

教科書では有効電力が別のやり方で導出されていますが、結果は一緒です。 瞬時電力ppを時間ttについて考えてみると、以下のことが言えます。

  • 第 1 項 VeIecos⁡θV_{e} I_{e} \cos\theta: ttを含まず、時間によない値。
  • 第 2 項 VeIecos⁡(2ωt−θ)V_{e} I_{e} \cos(2 \omega t - \theta): 電圧の周期の 2 倍で変化する値。1 周期の平均は零。

そして、第 1 項は定数項で、第 2 項は時間変化を伴う値で、全体としてはその 2 つの総和です。 グラフとしては、第 2 項 cos⁡(2ωt−θ)\cos (2 \omega t - \theta) を第 1 項 VeIecos⁡θV_{e} I_{e} \cos \theta のぶんだけ上にずらしたものといえます。

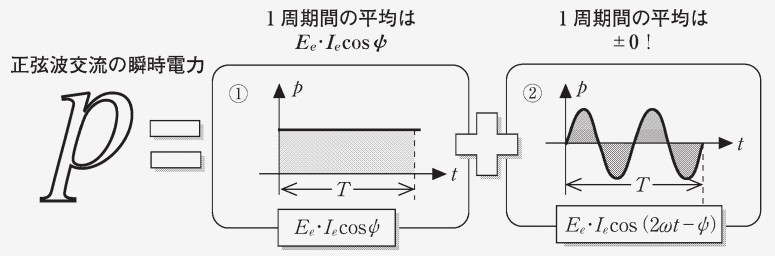
瞬時電力ppの 1 周期の平均値PeP_e（＝有効電力）は、上の図のように、第 1 項がVeIecos⁡θV_{e} I_{e} \cos\thetaで、第 2 項がθ=±0\theta = \plusmn 0となります。よって、有効電力Pe=VeIecos⁡θ\displaystyle P_e = V_{e} I_{e} \cos \thetaと導出できます。

有効電力の意味

有効電力の式について考えてみると、cos⁡θ=0\cos \theta = 0、つまり、θ=±π2\theta = \plusmn \frac{\pi}{2}のときに、有効電力は零となります。 θ=±π2\theta = \plusmn \frac{\pi}{2}となるインピーダンスzzは、抵抗RRが存在しないときです。 たとえば、第 11 回基本素子の交流回路で出てきたコンデンサのみを持つ交流回路やコイルのみを持つ交流回路です。 つまり、回路中に抵抗RRがまったく存在せず、コンデンサやコイルだけで構成されているときにこの条件が満たされます。 逆に言うと、有効電力は抵抗RRが存在するときにのみ発生します。 交流回路における実際の電力消費は、回路中の抵抗だけで起こっているとも言えます。

皮相電力と力率

有効電力からcos⁡θ\cos \thetaを除いた、VeIeV_e I_eの部分を皮相電力 (apparent power)と呼びます。 この値は、交流電源から供給される電力のことを指しており、電気機器にある電圧を掛けたときに瞬間的に何アンペアの最大電流が流れるかを算出するために利用されます。 皮相電力PaP_aの単位は[V⋅\cdotA] （ボルト・アンペア, volt-ampere）というものを用います。

  • 皮相電力 Pa=VeIeP_a = V_e I_e

また、cos⁡θ\cos \thetaの部分を力率と呼びます。 詳しくは複素ベクトルを用いた解析で述べますが、交流電源から供給された電力のうちのどれくらいが抵抗成分で実際に消費されるかを示しています。

  • 力率 =cos⁡θ= \cos \theta

複素ベクトルを用いた解析

ここからは、電力を複素ベクトルを用いて電力の計算を行い、交流回路の電力の理解を深めます。 具体的には、複素電圧V˙\dot{V}と複素電流I˙\dot{I}を用いて、複素数を用いて電力P˙\dot{P}を導出します。

まずは、前の節で示した回路と回路の電圧と電流を複素電圧V˙\dot{V}と複素電流I˙\dot{I}を用いて、複素形式での電力P˙\dot{P}を導出します。V˙\dot{V}とI˙\dot{I}は、複素数表記になっていますが、特性は前の節で用いたものと同一です。

  • 複素電圧: V˙\dot{V}。大きさはVeV_{e}。
  • 複素電流: I˙\dot{I}。大きさはIeI_{e}。電圧に対して位相がθ\thetaだけ遅れている。

この電圧と電流の複素ベクトルは以下のようになります。 説明の都合上、電流が基準になっていますが、電流が電圧に対してθ\thetaだけ遅れていることに変わりはありません。

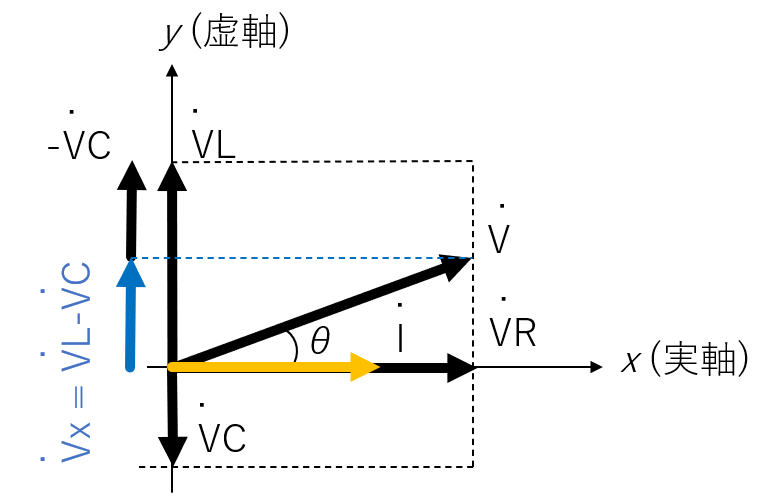
ここで、交流回路の複素電圧V˙\dot{V}は、コイルとコンデンサと抵抗に掛かる電圧の組み合わせから成ることを思い出してください。実軸は抵抗に掛かる電圧VR˙\dot{V_R}のみから成り、虚軸はコイルとコンデンサに掛かる電圧Vx˙=VL˙−VC˙\dot{V_x} = \dot{V_L} - \dot{V_C}からなります。逆に言うと、V˙\dot{V}はVR˙\dot{V_R}とVx˙\dot{V_x}に分解できます。

ここで、VR˙\dot{V_R}とVx˙\dot{V_x}をV˙\dot{V}で表すと、それぞれ以下のようになります。

  • 抵抗に掛かる電圧: VR˙=V˙⋅cos⁡θ\dot{V_R} = \dot{V} \cdot \cos \theta。大きさは、∣VR˙∣=Vecos⁡θ|\dot{V_R}| = V_e \cos \theta
  • コイルとコンデンサに掛かる電圧: Vx˙=V˙⋅sin⁡θ\dot{V_x} = \dot{V} \cdot \sin \theta。大きさは、∣Vx˙∣=Vesin⁡θ|\dot{V_x}| = V_e \sin \theta

VR˙\dot{V_R}とVx˙\dot{V_x}、V˙\dot{V}の関係を図にすると、以下のようになります。

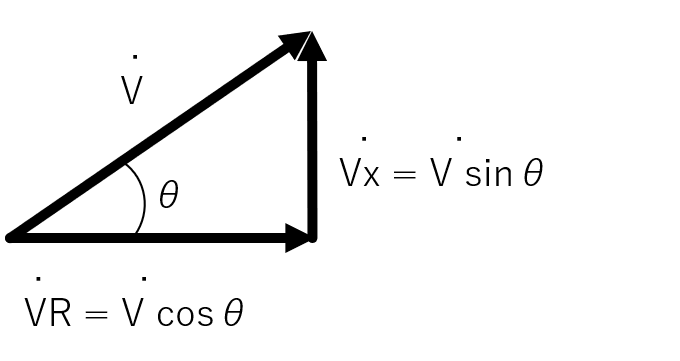
次に、2 つの電圧から発生する電力について考えてみます。

有効電力

抵抗で消費される電力PeP_eを考えてみます。ややこしいのですが、PeP_eは複素ベクトルではありません。 複素数空間でも電力は電流と電圧の積ですので、抵抗で発生する電力PeP_eは以下のように求められます。 そして、その大きさは、前の節で求めた有効電力の大きさPe=VeIecos⁡θP_e = V_{e} I_{e} \cos\thetaと一緒となります。

  • 抵抗で発生する電力 Pe=∣I˙∣∣VR˙∣=∣I˙∣∣V˙∣cos⁡θ=IeVecos⁡θP_e = |\dot{I}| |\dot{V_R}| = |\dot{I}| |\dot{V}| \cos \theta = I_{e} V_{e} \cos\theta

無効電力

コイルとコンデンサで消費される電力PrP_rを考えてみます。ややこしいのですが、PeP_eは複素ベクトルではありません。 PrP_rもPeP_eと同様に、電流と電圧の積で求められますので、以下のようになります。

  • コイルとコンデンサで消費される電力 Pr=∣I˙∣∣Vx˙∣=∣I˙∣∣V˙∣sin⁡θ=IeVesin⁡θP_r = |\dot{I}| |\dot{V_x}| = |\dot{I}| |\dot{V}| \sin \theta = I_{e} V_{e} \sin\theta

コイルとコンデンサで消費される電力PrP_rを、無効電力 (reactive power)と呼びます。 これは、コイルやコンデンサなどに一時的に蓄えられたエネルギーに対応した電力です。 つまり、無効電力は、電流の方向に伴い瞬間的には電力を消費していたり供給したりするが、実際は電源とコイルやコンデンサの間を行ったり来たりしているだけで、平均としては消費されない電力です。 無効電力の単位は [var] （バール, volt-ampere reactive）という単位を用います。 これは、有効電力[W]と区別するためです。

皮相電力と力率

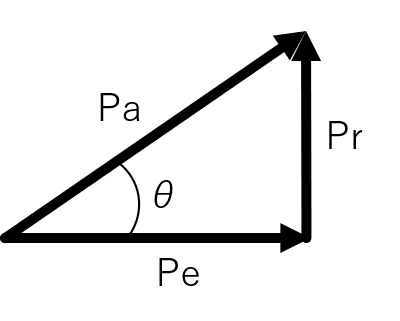
複素数平面では、皮相電力PaP_aと力率は、以下のように有効電力PeP_eと無効電力PrP_rから成る三角関数で表すことができます。 皮相電力の意味は、三角関数を用いた解析で述べたとおりです。

力率cos⁡θ\cos \thetaの角度を力率角θ=tan⁡−1(PrPe)\theta = \tan^{-1}{(\frac{P_r}{P_e})}と言います。 力率角θ\thetaは無効電力PrP_rと実効電力PeP_eの割合で、有効電力に対して無効電力が大きくなると、力率角も大きくなります。

力率の意味は、いくつか考えることができます。 皮相電力はその機器を動かすための電力であり、実際に利用される有効電力と実際には利用されていない無効電力を加えたものです。 つまり、無効電力が存在すると、必要以上に大きな電力が必要となり、そのために電気機器の電力容量を実際に利用される値よりも大きくしなければならない、と言えます。 また、交流電源から供給された電力のうちのどれくらいが抵抗成分で実際に消費されるかを示している、とも言えます。 力率が 1 になるように回路をうまく設計することを、力率改善と言います。

複素電力

ここまで出てきた三種類の電力（有効電力、無効電力、皮相電力）を複素ベクトルでうまく取り扱うために、複素電力という考え方が生み出されました。 ここではその説明を行います。

複素ベクトルでうまく取り扱うために、電流I˙\dot{I}の共役複素数I˙‾\overline{\dot{I}}を導入します。（唐突ですが…。） 共役複素数は、とあるベクトルとその大きさは一緒で、実軸に対して対称移動したベクトルのことです。 たとえば、a+jba + j bの共役複素数はa−jba - j bです。

この電流の共役複素数I˙‾\overline{\dot{I}}と電圧V˙\dot{V}のベクトル積を取ったものを複素電力Pc˙\dot{P_c}と定義します。

  • 複素電力 Pc˙=V˙I˙‾=Pe+jPr\dot{P_c} = \dot{V} \overline{\dot{I}} = P_e + j P_r

複素電力を電流I˙\dot{I}などほかの値を用いて表現すると以下のようになります。 なお、XXはリアクタンスです。

  • Pc˙=V˙I˙‾=Z˙I˙‾I˙=Z˙∣I˙∣2=(R+jX)∣I˙∣2=R∣I˙∣2+jX∣I˙∣2\dot{P_c} = \dot{V} \overline{\dot{I}} = \dot{Z} \overline{\dot{I}} \dot{I}= \dot{Z} |\dot{I}|^2 = (R + j X) |\dot{I}|^2 = R |\dot{I}|^2 + j X |\dot{I}|^2

電流の共役複素数I˙‾\overline{\dot{I}}を取る理由については、いろいろな議論があり、その意味を理解することは簡単ではありません。教科書の P.196 にも、共役複素数を掛ける意味が述べられていますが、そもそもなぜ共役複素数を掛ける必要があるのかは解説がありません。 参考になりそうなサイトを以下に列挙します。

  1. 有効電力・無効電力・複素電力│電気の神髄
  2. 理論計算の落とし穴(5)複素電力による有効電力・無効電力の計算 | 音声付き電気技術解説講座 | 公益社団法人 日本電気技術者協会
  3. 複素電力に複素共役が用いられる理由をインピーダンスとのアナロジーで解説 - Imaginary Dive!!
  4. 共役を感覚的に使い分けて複素電力を求めてみよう - 電験１種の棚卸し

とくに 1. 有効電力・無効電力・複素電力│電気の神髄では、共役複素数を掛ける理由が以下のように説明されています。これは私が知る範囲で一番もっともらしい理由です。（もっともらしい、というのは、単に私がこの説明の真偽を判断できていないだけです。）

演習問題

参考書 1 の P.101 例題 8.1
抵抗値 R=8R = 8[Ω\Omega]の抵抗、誘導性リアクタンス XL=11X_L = 11[Ω\Omega]のコイル、容量性リアクタンスXC=5X_C = 5[Ω\Omega]のコンデンサが、直列に接続された回路がある。 この回路に複素電圧V˙=100\dot{V} = 100[V]を加えた。回路を流れる電流I˙\dot{I}、皮相電力PaP_aと、有効電力PeP_e、無効電力PrP_r、および力率の大きさをそれぞれ求めよ。

参考書 1 の P.103 例題 8.2
ある交流回路に複素電圧V˙=200+j100\dot{V} = 200 + j 100[V]を加えたところ、複素電流I˙=8+j6\dot{I} = 8 + j 6[A]が流れた。 この回路のインピーダンスZ˙\dot{Z}、アドミタンスY˙\dot{Y}に加え、有効電力PP、皮相電力PaP_a、無効電力PrP_rの大きさをそれぞれ求めよ。

参考書 1 の P.104 演習問題 8.1 電力の諸量
ある交流回路に実効値が 100[V]の電圧を加えたところ、実効値が 30[A]の電流が流れ、負荷インピーダンスにおいて、1.8[kW]の電力が消費された。 力率、皮相電力、無効電力を求めよ。

参考書 1 の P.104 演習問題 8.2 RLC 直列回路の電力・リアクタンス表示
抵抗値 R=4R = 4[Ω\Omega]の抵抗、誘導性リアクタンス XL=18X_L = 18[Ω\Omega]のコイル、容量性リアクタンスXC=14X_C = 14[Ω\Omega]のコンデンサが、直列に接続された回路がある。 この回路に、複素電圧V˙=150\dot{V} = 150[V]を加えた。力率、皮相電力PaP_aと、有効電力PeP_e、無効電力PrP_rの大きさを求めよ。

参考書 1 の P.104 演習問題 8.3 RLC 直列回路の電力
抵抗値 R=50R = 50[Ω\Omega]の抵抗、インダクタンス L=200L = 200[mH]のコイル、キャパシタンスC=20C = 20[μ\muF]のコンデンサを接続したが RLC 直列回路に、実効値 100[V]、周波数 50[Hz]の電圧を加えた。 R, L, C を共通に流れる電流I˙\dot{I}を求めよ。 また、この回路の、力率、皮相電力PaP_aと、有効電力PeP_e、無効電力PrP_rの大きさを求めよ。

参考書 1 の P.104 演習問題 8.4 RLC 並列回路の電力
抵抗値 R=25R = 25[Ω\Omega]の抵抗、誘導性リアクタンス XL=40X_L = 40[Ω\Omega]のコイル、容量性リアクタンスXC=20X_C = 20[Ω\Omega]のコンデンサを接続したが RLC 並列回路に、実効値 100[V]の電圧を加えた。 合成インピーダンスZ˙\dot{Z}を流れる電流I˙\dot{I}を求めよ。 また、この回路の、力率、皮相電力PaP_aと、有効電力PeP_e、無効電力PrP_rの大きさを求めよ。

参考書 1 の P.104 演習問題 8.5 複素電力
インピーダンスZ˙=40−j30\dot{Z} = 40 - j 30[Ω\Omega]をもつ回路に、複素電圧V˙=200+j100\dot{V} = 200 + j 100[V]を加えた。 この回路に流れる電流I˙\dot{I}、複素電力PcP_c、皮相電力PaP_aと、有効電力PeP_e、無効電力PrP_rの大きさを求めよ。