コンテンツにスキップ

第9回 交流回路の基礎知識

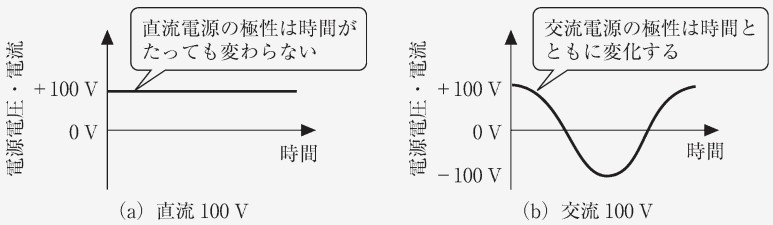
ここからは、交流回路を取り扱っていきます。交流回路とは、交流の電流源と電圧源を持つものになります。 ここまで学んできた直流回路では、電源電圧・電流の方向は時間にかかわらず一定でした。 対して、交流回路では、電源電圧・電流の方向が周期的に変化します。これによって、効率的な電気の送受信や回路の効率化が可能になるのですが、回路の解析は格段にたいへんになります。具体的には、微分や積分、三角関数を多様することになります。今回は、交流回路の解析に必要な基礎知識について述べていきます。

交流電源とは

ここでは、交流電源の概要について述べていきます。

概要

  • 定義: 交流回路とは、交流の電圧源や電流源を持ち、交流の電圧や電流が印加・流れる回路のこと

交流の電圧源や電流源では、電圧や電流の大きさが周期的に変化します。この講義の中では、周期的な変化のパターンは、もっとも一般的な正弦波（sin 波）のみを取り扱います。

正弦波交流電圧をグラフに表すと以下のようになります。 縦軸が電圧vv[V]、横軸が時間ttで、このグラフでは、以下の用語が示されています。

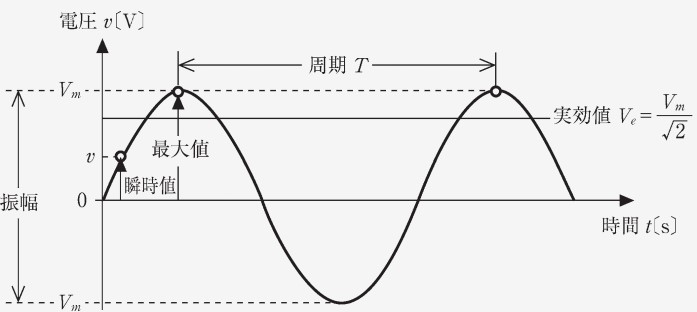
  • 瞬時値 vv[V]: ある任意の時間における電圧の大きさ。VmV_m～−Vm-V_m
  • 最大値 VmV_m[V]: 最大の振幅となる電圧の大きさ。
  • 実効値 VeV_e[V]: 最大値を2\sqrt2で割った電圧の大きさ。Vm=Ve2V_m = \frac{V_e}{\sqrt2}
  • 周期 TT[s]: 正弦波交流電圧の周期。角速度をω\omegaとすると、ωT\omega T[rad]ともできる。
  • 周波数 ff[Hz]: 1 秒間での周期の繰り返し回数(f=1Tf = \frac{1}{T})

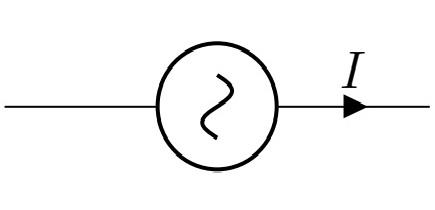
回路記号は以下の 2 つになります。

  • 正弦波交流電圧源:
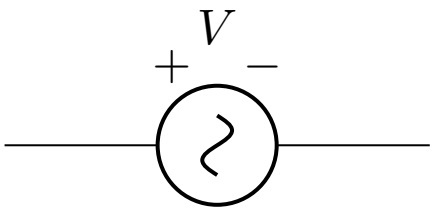
  • 正弦波交流電流源: （VVがないと、見分けがつかない…。本講義では扱わない）

発生原理

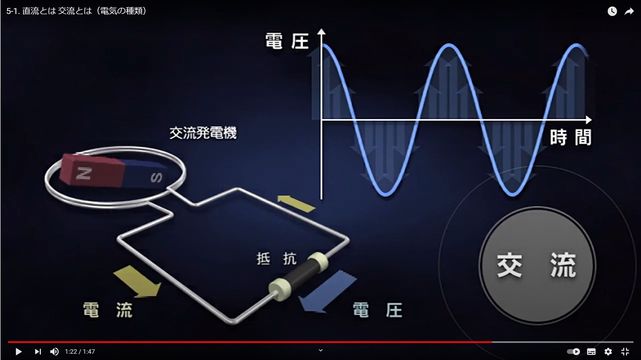
ここでは、なぜ交流電圧が発生するのかを発電という点から見ていきます。以下の動画では、交流電圧が発生する理由がわかりやすく説明されています。

多くの発電機は、何かしらのエネルギーを用いて電磁石（タービン）を回します。 上記の動画より抜き出した、以下の画像の左下の「交流発電機」がその部分になります。ここから電磁気力で電圧が発生しますが、電磁石自体が回転しているため、発生する電圧は右上の図のように周期性を持った交流電圧となります。

また、三相交流電圧が発生するしくみと発電機のしくみについては、以下の動画が参考になります。

利用例

一般家庭のコンセントには、100V の交流電圧が供給されています。情報科学科のみなさんが扱うであろう範囲では、以下の 3 つの交流電源が存在します。

  1. 単相 100V 交流電源
  2. 単相 200V 交流電源
  3. 三相 200V 交流電源

単相 100V や 200V の交流電源は、コンセントを介して PC やサーバなどの大型計算機に直接的に電源として供給されています。また、三相 200V の交流電源は、データセンターのサーバラックに搭載された複数の機器への大元の電源として使用されています。

コンセントの形状が少し違うので、電源ケーブルを間違って刺すことはないと思います。 が、間違った電源ケーブルを買ってきて、刺さらない…、ということは良くあります :P


単相100V直流電源, 単相200V直流電源, 三相200V交流電源のコンセント形状

CPU やメモリなど計算機の多くの部品は直流回路ですが、計算機の電源は単相 100V 交流電源です。計算機の電源には、交流電圧を直流電圧に変換する機能が搭載されています。この直流と交流の変換機のことをコンバータと言い、直流から交流への変換効率が高ければ高いほど、良いコンバータとされています。たとえば、スマートフォンの AC アダプタはコンバータの一種です。効率が悪い AC アダプタが熱を持ってしまうのは、直流から交流への変換効率が低く、変換できなかったエネルギーが熱になってしまうためです。

近年、電力効率を追求するために、データセンターを自社で設計するケースも増えてきています。 データセンターでは、発電所などから供給される高電圧の交流の電気を単相 100V に変換する必要があり、電気回路の知識が役に立ちます。 なお、直流から直流の変換器のことをコンバータと言います。 高い電力効率の達成には、電気回路やコンバータのような情報科学以外の分野も広く知っておかなければなりません。

以下に、データセンターと電源についての図を示します。この図のデータセンターでは、以下の経路で電気が供給されています。

  1. 変電所からの引き込み。交流 6600V, 2 万 2000V, 6 万 6000V
  2. 受変電装置、自家発電装置。交流 415V
  3. 変圧器。交流 200V or 100V


データセンターのネットワークと電源の概要 出典: 第3回　データセンターのネットワークと電源 | 日経クロステック（xTECH）

たとえば、理化学研究所計算科学研究センターのスーパーコンピュータ富岳では、6900V の交流高電圧を引き込み、トランスで 200V の交流電圧に落としています。
FUGAKU NEWS vol.3　設備工事 - YouTube
計算機棟の施設の3Dモデル

また、さくらインターネットの自社データセンター（北海道石狩市）では、電力効率の向上のために HVDC(High Voltage Direct Current)と呼ばれる、高電圧の直流給電方式を採用しています。HVDC は、300V を超える高電圧直流を集中電源で 12V などへと降圧したうえで、そのままサーバに給電する方式です。これにより、直流交流変換が一度で済むため、総合的な効率は 90％以上となり、従来の AC 方式と比較して画期的な電力効率が実現可能とのことです。
電力効率の向上 - データセンター紹介｜企業情報｜さくらインターネット

正弦波交流電源に出てくる値

ここからは、正弦波交流電源のモデル化（定式化）を行い、実効値 (effective value)と位相 (phase)について少し詳しく説明します。

モデル化

前述のように、正弦波交流電圧源の電圧は以下のような時間変化を示します。

  • 瞬時値 vv[V]: ある任意の時間における電圧の大きさ。VmV_m～−Vm-V_m
  • 最大値 VmV_m[V]: 最大の振幅となる電圧の大きさ。
  • 実効値 VeV_e[V]: 最大値を2\sqrt2で割った電圧の大きさ。Vm=Ve2V_m = \frac{V_e}{\sqrt2}
  • 周期 TT[s]: ある値に戻るまでの時間。正弦波交流電圧の周期。
  • 周波数 ff[Hz]: 1 秒間での周期の繰り返し回数。f=1T=ω2πf = \frac{1}{T} = \frac{\omega}{2 \pi}

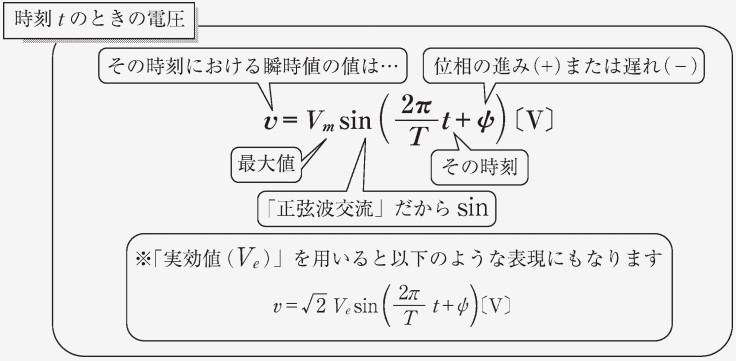
この時間変化を三角関数を用いてモデル化すると、瞬時値v(t)v(t)は時間の関数となり、以下の式で表すことができます。

  • 瞬時値: v(t)=Vmsin⁡(2πTt+ϕ)v(t) = V_m \sin \left( \frac{2\pi}{T} t + \phi \right)

また、後述の角周波数と周期の関係を用いて、以下のように書くこともできます。

  • 瞬時値: v(t)=Vmsin⁡(2πTt+ϕ)=Vmsin⁡(ωt+ϕ)v(t) = V_m \sin \left( \frac{2\pi}{T} t + \phi \right) = V_m \sin \left( \omega t + \phi \right)

教科書の P.113 にそれぞれの項の意味するところが述べられています。2πT\frac{2\pi}{T}は角周波数（=角速度）と呼ばれ、周期の変化の速さを示しています。

正弦波曲線と回転運動

ここでは、簡単に正弦波曲線と回転運動の関係について述べたあと、電圧の変化の速度が角周波数として考えられる理由について述べます。

上記の正弦波曲線のグラフは、電圧と時刻の関係を図示したものでした。 この正弦波曲線の電圧の挙動、電磁石の回転運動から出てきたものです。 回転運動の図は、電圧と座標の関係を示したものになります。 ですので、両者は同じものを別の観点から見たものと言えます。

電圧と回転運動の関係について考えるために、以下の図を導入します。 これは、点 P が半径VmV_mの円周上を毎秒nn回転したものです。 点 P が 1 回転すると、正弦波曲線は 1 周期分を描くことになり、回転運動と正弦波曲線とは 1 対 1 の関係になっています。 このyy座標を時間の経過に従って描いたものが正弦波曲線と言えます。


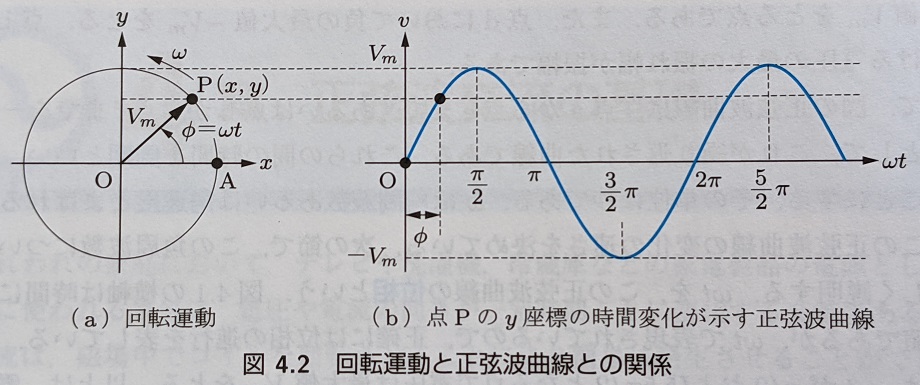
出典: 参考書 P.46

回転運動における回転の速さをnn[s−1s^{-1}]とすると、回転角度の速さ、すなわち角周波数ω\omegaは以下のように表されます。

  • 角周波数: ω=2πn\omega = 2 \pi n[rad/s]

また、この角周波数ω\omegaで、tt秒間経過したときの回転角ϕ\phiは以下のようになります。

  • 回転角: ϕ=ωt\phi = \omega t[rad]

よって、半径VmV_mの円周上を角周波数ω\omegaで回転する点 P のyy座標は、以下の式で表せます。これは、正弦波曲線を時刻の経過に従って描いた正弦波曲線と同じものです。

  • 点 P のyy座標: y=Vmsin⁡ϕ=Vmsin⁡ωty = V_m \sin \phi = V_m \sin \omega t

電圧の変化の速度は、角周波数として考えることができます。 そして、角周波数は、周期や周波数と以下のような関係があるため、電圧の変化をこれらを使って表すことがあります。

  • 角周波数ω\omegaと周期TTの関係：ω=2πT\omega = \frac{2\pi}{T}[rad/s]
    　これは、1 回転は2π2 \pi[rad]ですので、それを周期TTで割ったものが角周波数ω\omegaになる、という意味です。
  • 角周波数ω\omegaと周波数ffの関係: f=ω2π=2πff = \frac{\omega}{2 \pi} = 2 \pi f
    　これは、1 回転は2π2 \pi[rad]ですので、角周波数ω\omegaを2π2\piで割ったものが周波数ffになる、という意味です。
  • 周期TTと角周波数ω\omegaの関係：T=2πωT = \frac{2\pi}{\omega}[rad/s]
    　これは、1 回転は2π2 \pi[rad]ですので、それを角周波数ω\omegaで割ったものが周期TTになる、という意味です。

位相 ϕ\phiについては、本ページの後半で解説します。

実効値

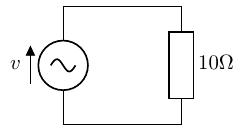
実効値は、「その交流電圧を直流電圧に換算した場合に、実際に仕事として効力が出る値」という意味になります。 逆に考えると、ある直流電圧と同じ仕事ができる交流電圧の値（＝実行値）を知りたい、と言えるので、イメージとしては以下のような形になります。直流電圧源を持つ左の回路と同じ仕事ができるように、右の回路の交流電圧源の値を設定します。

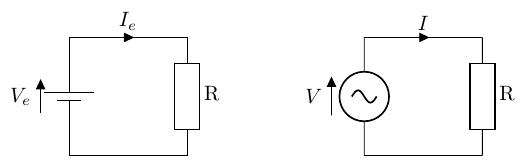
実効値は以下のように、最大値の2\sqrt 2分の 1 となります。

  • 実効値 Ve=Vm2V_e = \frac{V_m}{\sqrt 2}

実効値を考えることによって、交流の電圧源・電流源を直流のそれと同じ様に考えることができます。たとえば、家庭用電源の 100[V]は実効値を示しています。ですので、この電源が流す最大値は、100 ×2\times \sqrt 2 = 141.4[V]になります。

実効値をVrmsV_{rms}とすることがあります。これは、Root Mean Square value（2 乗平均平方根値）の略で、それぞれ Root=ルート、Mean=平均、Square=2 乗、value=値という意味です。

また、実効値は平均値ではないことにも注意してください。交流電圧および交流電流の大きさは平均値ではなく実効値で表すのが一般的です。

実効値の導出

ここから、実効値を頑張って導出してみますが、覚えたほうが早いと思います。
また、教科書では同様のことが、以下のように図を用いて直感的に示されています。

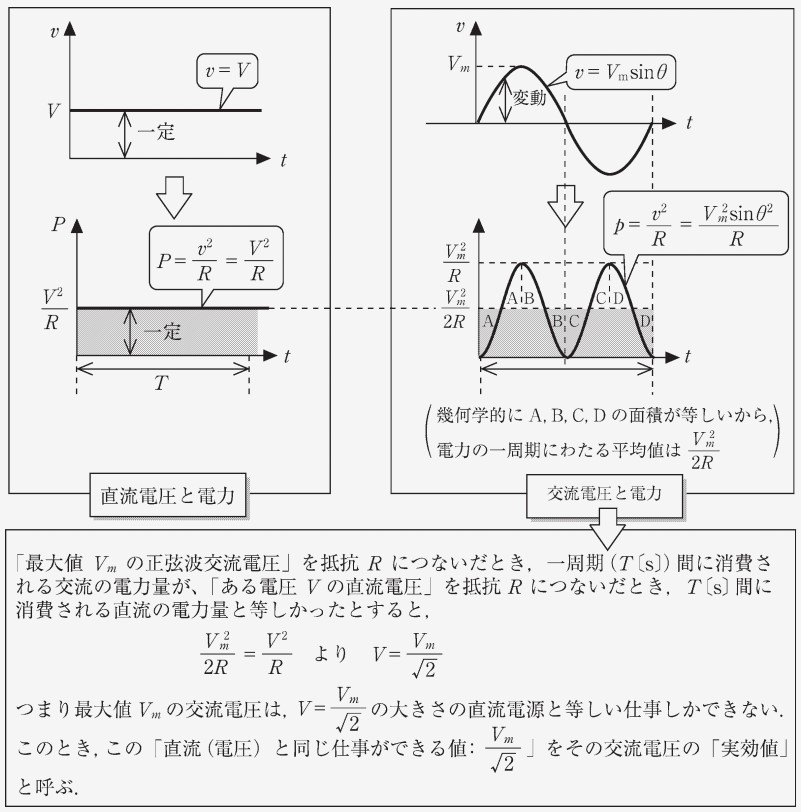
実際に行う仕事の量、つまり電力、の観点からの話ですので、両者の電力が同じになる様な電圧を計算します。単位時間TTでの両者の電力は、それぞれ以下のようになります。

  • 直流回路の電力: Pdc=Ve2RP_{dc} = \frac{V_e^2}{R}
  • 交流回路の電力: Pac=v(t)2RP_{ac} = \frac{v(t)^2}{R}

PacP_{ac}の積算電力は以下のように算出します。簡単化のために、ϕ=0\phi = 0としています。

Pac=∫0Tv(t)2R=1R∫0T{Vmsin⁡(ωt+ϕ)}2=Vm2R∫0Tsin⁡(ωt+ϕ)2=Vm2R∫0Tsin⁡2ωt=Vm2R∫0T(1−cos2ωt)2=Vm22R∫0T(1−cos2ωt)=Vm22R−Vm22∫0T(cos2ωt)=Vm22R−0=Vm22R\displaystyle P_{ac} = \int_{0}^{T} \frac{v(t)^2}{R} = \frac{1}{R} \int_{0}^{T} \left\{V_m \sin \left( \omega t + \phi \right) \right\}^2 = \frac{V_m^2}{R} \int_{0}^{T} \sin(\omega t + \phi)^2 \\ = \frac{V_m^2}{R} \int_{0}^{T} \sin^2 \omega t = \frac{V_m^2}{R} \int_{0}^{T} \frac{(1-cos2 \omega t)}{2} = \frac{V_m^2}{2R} \int_{0}^{T} (1-cos2 \omega t) \\ = \frac{V_m^2}{2R} - \frac{V_m^2}{2} \int_{0}^{T} (cos2 \omega t) = \frac{V_m^2}{2R} - 0 = \frac{V_m^2}{2R}

直流回路の電力 == 交流回路の電力とする場合は、以下のようになる。
（→\rightarrowに特に数学的な意味はありません。改行すると見栄えが悪くなるため、改行の代わりに使っています。）
Pdc=Pac→Ve2R=v(t)2R→Ve2R=Vm22R→Ve=Vm2\displaystyle P_{dc} = P_{ac} \rightarrow \frac{V_e^2}{R} = \frac{v(t)^2}{R} \rightarrow \frac{V_e^2}{R} = \frac{V_m^2}{2R} \rightarrow V_e = \frac{V_m}{\sqrt 2}

よって、Pdc=PacP_{dc} = P_{ac}になるときの電圧VeV_eは、Ve=Vm2V_e = \frac{V_m}{\sqrt{2}}となり、これを実行値と呼んでいます。

位相

位相は、複数の交流電圧源を回路に接続した場合に登場する概念です。

以下の図のように、2 つの交流電圧源の時間方向の差分を位相差と呼びます。 つまり、位相ϕ\phiは、ある交流電圧が基準の正弦交流波とどのくらいズレているかを示す値になります。教科書 P.113 では 2 つのゴンドラを用いて具体的に位相のイメージが説明されていますので、ぜひ読んでください。

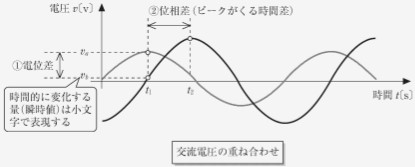
本講義では直接扱いませんが、三相交流回路では位相がとても重要な役割を果たします。 三相交流は、位相がそれぞれ 120°ずれた 3 つの交流電圧を用いて全体の瞬時電圧を零にして、回路の効率化を行ています。

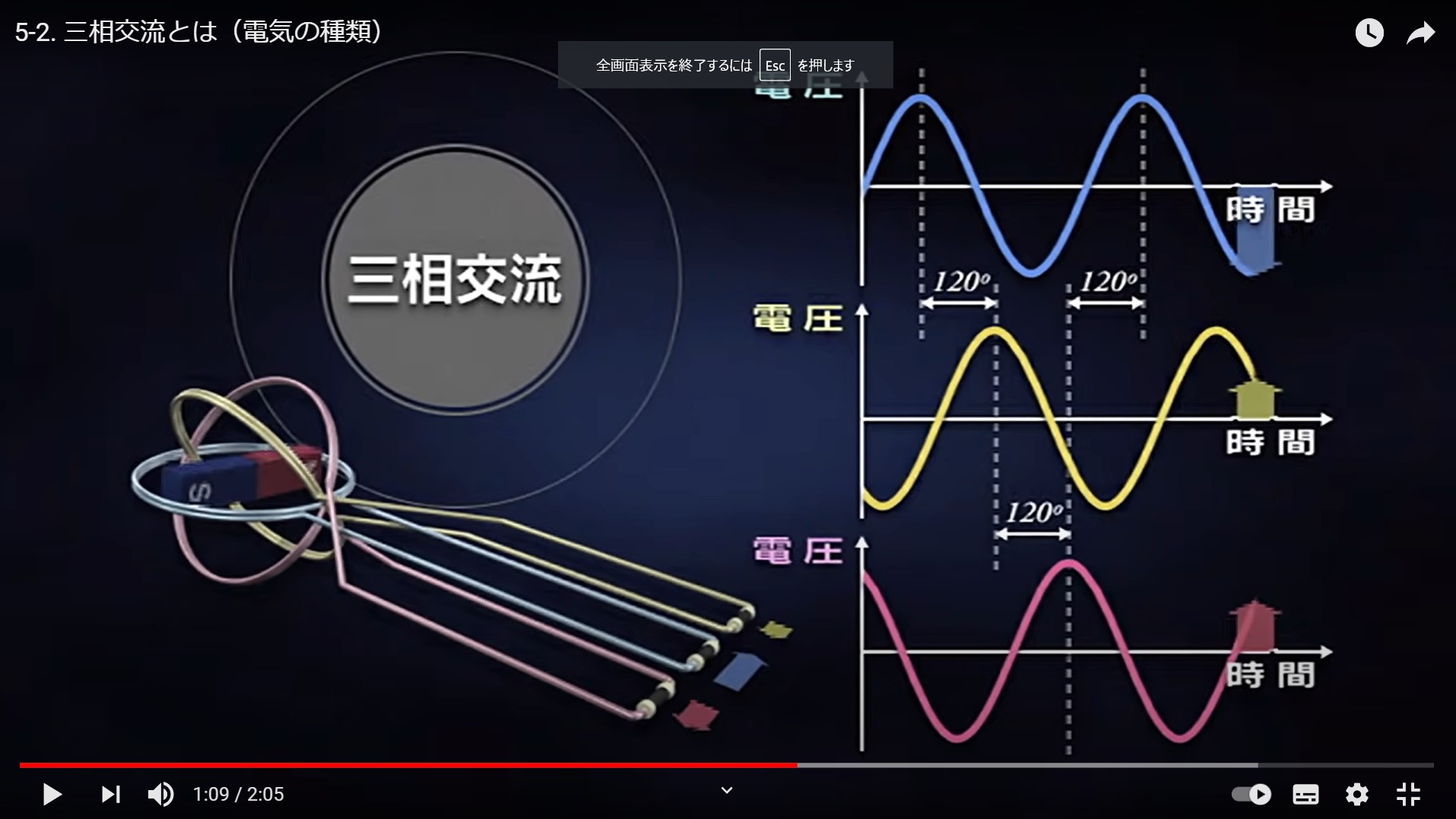
5-2. 三相交流とは（電気の種類） - 東京電力グループ - YouTube

演習問題

演習問題 6.1

v=100sin⁡(50πt−π3)\displaystyle v = 100 \sin (50 \pi t - \frac{\pi}{3})[V]について、最大値VmV_m[V]、実効値VeV_e[V]、角周波数ω\omega[rad/s]、周期TT[s]、周波数ff[Hz]、位相角ϕ\phi[rad]を求めよ。

演習問題 6.2

Warning

最後の行のv2v_2とv1v_1が逆のようです。説明はあっていると思われます。

  • 誤: したがって、図よりv2v_2がv1v_1に対してπ2\frac{\pi}{2}[rad]だけ位相が進んでいる。
  • 正: したがって、図よりv1v_1がv2v_2に対してπ2\frac{\pi}{2}[rad]だけ位相が進んでいる。

演習問題 6.3

次の回路で抵抗RRに流れる電流の瞬時値と実効値を求めよ。
なお、交流電圧源は以下の式で表されるものとする。
v=2⋅100sin⁡(50πt−π3)\displaystyle v = \sqrt2 \cdot 100 \sin (50 \pi t - \frac{\pi}{3})[V]