第5回 コンダクタンス、電流源と電圧源

今回は、より複雑な回路を解くための準備として、コンダクタンス(Conductance)と電流源(Current source)と電圧源(Voltage source)について述べていきます。コンダクタンスは、計算を簡単にするために導入するもので、抵抗の逆数ですので、それほど難しくはありません。電流源と電圧源は、それ自体はわかりやすいですが、両者を等価変換する際に注意が必要です。等価変換は、慣れてしまえば機械的に変換できるようになるはずです。

コンダクタンス

コンダクタンスは、電気回路における電流の流れやすさを示す値です。抵抗が電流の流れにくさを示す値ですので、それの逆の意味を持ちます。

定義

コンダクタンスの定義

直流回路では抵抗の逆数とする。また、交流回路ではインピーダンスの逆数の実数部とする。

コンダクタンスの単位

[$S$] (siemens, ジーメンス)の定義* 直流回路では、1[$S$]とは、$\displaystyle 1[S] = \frac{1}{1[\Omega]}$。

オームの法則をコンダクタンスを用いて表すと以下のようになります。

$$\displaystyle E = I R = \frac{I}{G}$$

適用例

コンダクタンスは電気抵抗の逆数の値ですので、抵抗を並列接続した回路を解析する際に使用すると計算が楽になります。特に、分流を求めるときに有効なツールです。なお、抵抗の直列接続の計算には無理にコンダクタンスを使う必要はありません。抵抗$R[\Omega]$を引き続き使っても大丈夫ですが、抵抗とコンダクタンスを混ぜる際は単位$[S]$と$[\Omega]$に注意してください。

教科書 P.40 の以下の図では、抵抗の並列接続の合成抵抗をレジスタンス$R$とコンダクタンス$G$を用いて表しています。コンダクタンスを使用することで、分数の計算がなくなり、計算がシンプルになります。

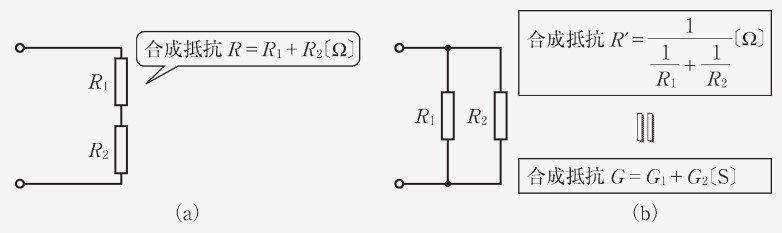
合成抵抗の計算

演習 3.4 の回路について考えてみます。まず、合成コンダクタンス$G$を求めます。

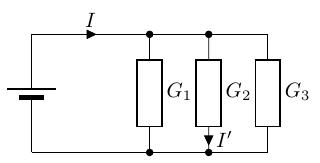
まずは、レジスタンスで考えます。 並列接続された抵抗なので合成抵抗$R$は、以下の値になります。

$$\displaystyle \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$

ここで、コンダクタンスの定義より、$G = \frac{1}{R}, G_1 = \frac{1}{R_1}, G_2 = \frac{1}{R_2}, G_3 = \frac{1}{R_3}$とできます。

よって、合成コンダクタンス $G$は以下のような、単純な総和の形となります。

$$G = G_1 + G_2 + G_3$$

分流の計算

次に、この回路の$G_2$に流れる電流$I'$を求めてみます。つまり、分流の計算です。

抵抗の並列接続のぶん流は、抵抗で表すと以下の値になります。つまり、合成抵抗に対する$G_2$部分の抵抗の割合です。

$$I' = \frac{\frac{1}{R}}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}} I$$

これに各コンダクタンスを代入すると、以下の式となり、単純な割合として示すことができます。

$$I' = \frac{G_2}{G_1 + G_2 + G_3} I$$

このように、コンダクタンスを導入することによって、抵抗の並列接続の計算が簡単になります。

演習問題 3.5

演習問題 3.5 「次の回路で$G_4$に流れる電流の大きさを求めよ。」をやってみましょう。 抵抗とコンダクタンスを混ぜてもかまいませんが、混ぜる場合は単位に注意してください。

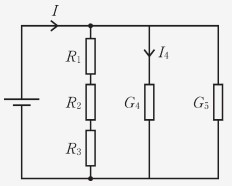
追加問題

演習 1.4 のすべての回路のコンダクタンス$[S]$を求めてみましょう。 ただし、$R_1=10[\Omega], R_2=20[\Omega], R_3=40[\Omega]$とします。

• 回路 (a)
  

• 回路 (b)
  

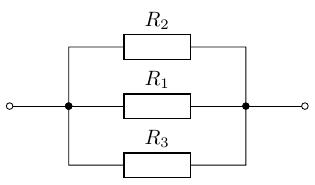
• 回路 (c)
  

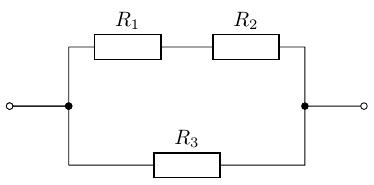
• 回路 (d)
  

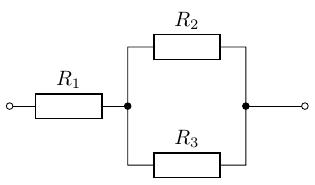
電流源と電圧源

電流源 (Voltage source) と電圧源 (Current source) は、その名の通り、電流の源となるもの、電圧の源となるものです。これまでの講義では、乾電池などの直流の電圧源のみを電圧源として扱ってきました。ここでは電流源を新たに導入し、その取り扱いについて述べます。

定義

電圧源

電圧源の定義

一定の直流もしくは交流の電圧を発生させるもの。本講義で扱う電圧源は、すべて理想電圧源とする。また、直流の理想電圧源(理想定電圧源)の回路記号は、以下である。

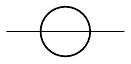
JIS 記号の理想定電圧源

直流の電圧源を定電圧源とも言います。また、理想定電圧源は、平たく言うと、その電圧源から流れる電流がたとえ 0[A]でも 100 万[A]になろうとも、何が何でも一定の電圧を保ち続けるものです。なお、これまでは電源を理想電圧源としていましたので、引き続き、電源を理想電圧源として取り扱います。

電流源

電流源の定義

一定の直流もしくは交流の電流を発生させるもの。本講義で扱う電流源は、すべて理想電流源とする。また、直流の理想電流源(理想定電流源)の回路記号は、以下である。

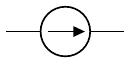
旧 JIS 記号の理想定電流源

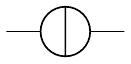
新 JIS 記号の理想定電流源

直流の電流源を定電流源とも言います。理想定電流源は、平たく言うと、その電流源にかかる電圧がたとえ 0[V]でも 100 万[V]になろうとも、何が何でも一定の電流を保ち続けるものです。

実用上の取り扱いで注意する点として、電圧源は、直列接続はできるが、並列接続はできません。電流が逆流してしまいます。 逆に、電流源は、直列接続はできないが、並列接続はできます。電流が不安定になってしまいます。 やってはいけない接続方法でつなぐと、逆電流や過電流の原因となり、回路全体が壊れてしまいます。 なぜそうなのかの具体的な話は、教科書の P.50 3.2.2, 3.2.3 を読んでみてください。

	直列接続	並列接続
電圧源	OK	NG
電流源	NG	OK

また、理想電流源と理想電圧源と、実際の電流源と電圧源は、実際に流せる電流や印加できる電圧に差ができてしまいます。 これは、実際の電流源や電圧源には内部抵抗が存在するからです。 電流源の場合、それにかかる電圧が高くなれば高くなるほど、内部抵抗に流れる電流も大きくなります。そのため、電流源から流せる実際の電流はそのぶんだけ小さくなります。 また、電圧源の場合、流す電流が大きくなれば大きくなるほど、オームの法則により、内部抵抗での電圧降下が大きくなってしまいます。そのため、電圧源で印加できる実際の電圧は低くなってしまいます。

等価変換

ここでは、電流源と電圧源が等価変換できることを示します。 教科書 P.52 の以下の 2 つの回路において、負荷$R$の両端にかかる電位差$V$と$V'$について考えてみます。 ①が電圧源を持った回路で、②が電流源を持った回路です。

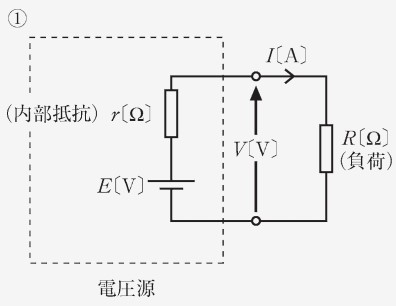
まず、①の点線で囲われた「電圧源」の部分は、理想定電圧源$E[V]$に内部抵抗$r[\Omega]$が直列接続され、実際の電圧源を模擬しています。

負荷$R$の両端にかかる電位差$V$は、以下のようになります。

$$\begin{align} I &= \frac{E}{R+r} \\ V &= RI = R\frac{E}{R+r} \end{align}$$

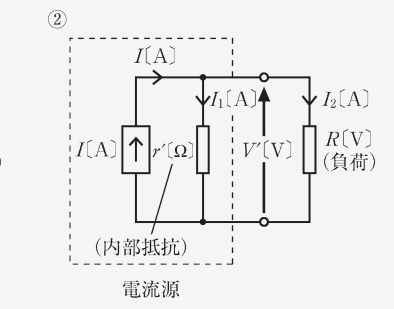
また、②の点線で囲われた「電流源」の部分は、理想定電流源$I[A]$に内部抵抗$r'[\Omega]$が並列接続され、実際の電流源を模擬しています。

負荷$R$の両端にかかる電位差$V'$は、以下のようになります。

$$\begin{align} I &= I_1 + I_2 = \frac{V'}{r'} + \frac{V'}{R} = (\frac{1}{r'}+\frac{1}{R}) V' \\ V' &= \frac{I}{ \frac{1}{r'} + \frac{1}{R} }= \frac{R}{R+r'} r' I \end{align}$$

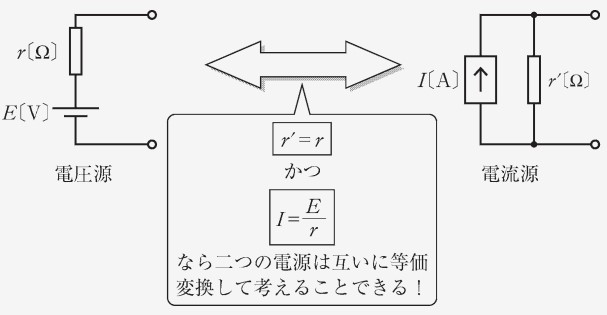
ここで、両者を見比べると $r' = r$かつ$E = {I}{r'}$のとき、$V=V'$となります。つまり、2 つの回路が等価になります。

これを一般化すると、「以下の 2 点は同一のものであり、相互に等価変換ができる」と言えます。

• 起電圧 $E[V]$で、内部抵抗$r[\Omega]$の定電圧源
• 起電流 $I=\frac{E}{r}[A]$で、内部抵抗$r[\Omega]$の定電流源

適用例

以下の電流源の回路と等価な電圧源回路を示してみます。

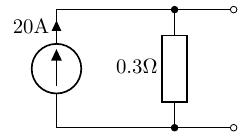
電流源を電圧源に等価変換するので、$I=\frac{E}{r}$が成り立てば良いわけです。 つまり、

$$\begin{align} I &= \frac{E}{r} \\ 20 &= \frac{E}{0.3} \\ E &= 20 \times 0.3 \\ &= 6 \end{align}$$

回路図としては、以下のものとなります。

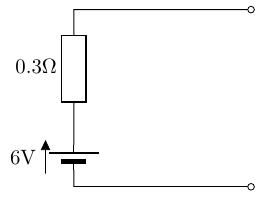
電流源の回路のシミュレーション結果 と その等価な電圧源の回路のシミュレーション結果

追加問題

• 以下の電圧源の回路と等価な電流源回路を図示せ。また、その回路の電流源$I$と内部抵抗のコンダクタンス$G$も求めよ。
  

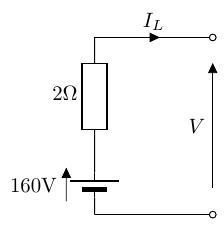
コンダクタンスと電流源、電圧源の組み合わせ

今回述べた、コンダクタンスと電流源、電圧源を組み合わせた回路を考えてみます。 例題 3.1 の回路は一見複雑に見えますが、等価変換とコンダクタンスを用いてシンプルな回路に変換した後、電流を求めることができます。

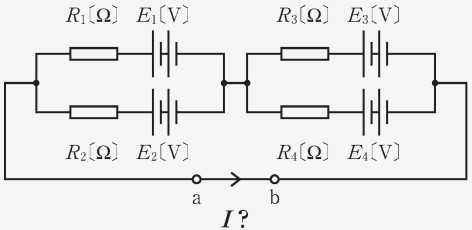
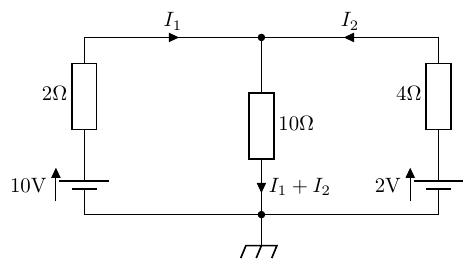
例題 3.1

「次の回路の枝路 a-b 間に流れる電流を求めよ。」

教科書 P.55 の「電圧源は並列接続できない。そこで…」とは、詳しくは、「電圧源は並列接続できないので、回路を整理して 1 つにまとめることができない。そこで、電圧源を電流源を等価変換し、電流源をひとまとめにして回路を整理できるようにします。」という意味になります。

教科書 P.56 の最後の式が間違っているようです。「ただし、」の 1 つうえの式の最後の部分は、分母が$G_A G_B$ではなく、$G_A + G_B$です。正確には以下の値になります。
見つけてくれてありがとう :)

• 誤: $\frac{G_B I_A + G_A I_B}{G_A G_B}$

• 正: $\frac{G_B I_A + G_A I_B}{G_A + G_B}$

追加問題

• 以下の回路の電流$I_1 + I_2$を、電圧源を電流源に変換しつつ求めよ。
  キルヒホッフの法則の回の適用例で出てきた問題と同一ですが、等価変換を用いて解くことができます。
  
  シミュレーション結果