第4回 キルヒホッフの法則

キルヒホッフの電流則と電圧則

今回は、より複雑な電気回路を扱うための キルヒホッフの電流則とキルヒホッフの電圧則 について定義と解説、使い方の説明を行います。
オームの法則とキルヒホッフの電流則と電圧則を用いることで、ほぼすべての電気回路を解析できます。
キルヒホッフの法則は、高校で学んだほうもいると思いますが、とても重要な法則ですのであらためて理解してみてください。

キルヒホッフの電流則 (第1法則)

ここでは、キルヒホッフの電流則 (第 1 法則)の定義と使い方、適用例について述べていきます。

定義とその解説

キルヒホッフの電流則 (第 1 法則) の定義

電気回路のある節点に流入する電流の総和はゼロである。

数式で表すと以下のようになります。これをある接点における接点方程式と呼びます。なお、$I$は各枝路の電流とします。

$$\sum_{k=1}^{n} I_{k} = 0$$

基本的には、ある節点でのエネルギー保存を意味していますので、以下のように言い換えることができます。

キルヒホッフの電流則 (第 1 法則)の言い換え

電気回路のある節点に流入する電流の総和と流出する電流の総和は等しい。

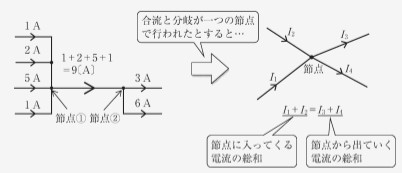
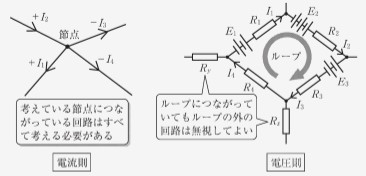
ある節点にいくつの枝路が出入りしていてもこの法則は成り立ちます。
図の右の回路のように節点が十字路のようになっている場合は、図の左の回路のように分解して考えるとわかり易いです。

使い方

キルヒホッフの電流則 (第 1 法則)を用いて各節点の電位を求める手順は、次の通りです。
教科書の P.25 には 1～3 までのステップが示されていますが、4 と 5 も追加すると手順が明確になると思います。

1. 電圧の基準点を決める
2. その基準点に対する各節点の電位 $V_1, V_2$などを仮定する。また、必要であれば、各枝路の電流 $I_1, I_2$なども仮定する。
3. 基準点と起電力がそのまま掛かっている点を除く各節点について、キルヒホッフの電流則を適用し、節点方程式を立てる。
4. $n - 1$ 個の節点方程式を立てるまで、3 を繰り返す。なお、$n$は節点の数である
5. 立てた節点方程式を各節点の電位について解く

節点方程式は、着目している節点以外の部分を無視できる点もポイントです。

適用例

教科書 P.23 の例と同一である、P.31 の例題 2.1 をキルヒホッフの電流則を使って問いてみます。
「次の回路の接点の電圧$V_1, V_2$をキルヒホッフの電流則を用いて求めよ。」

シミュレーション結果

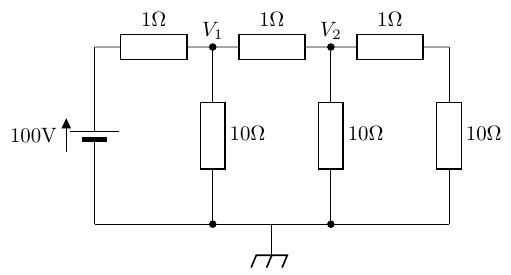
教科書 P.26 の回路をキルヒホッフの電流則を使って問いてみます。
「次の回路に流れる電流$I_1, I_2$をキルヒホッフの電流則を用いて求めよ。」

シミュレーション結果

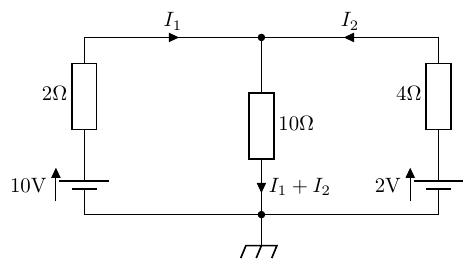
演習問題 2.1

教科書 P.35 の演習問題 2.1 をキルヒホッフの電流則を使って問いてみましょう。

シミュレーション結果

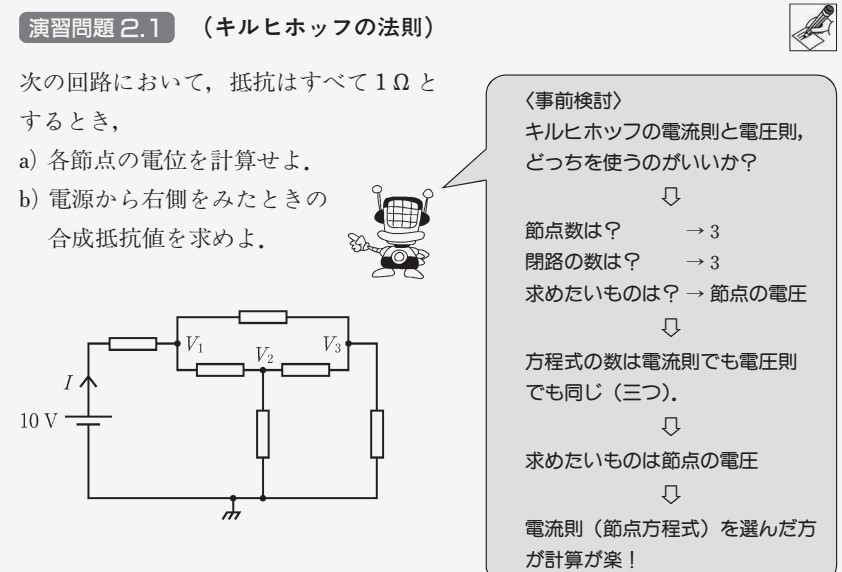
キルヒホッフの電圧則 (第2法則)

ここでは、キルヒホッフの電圧則 (第 2 法則)の定義と使い方、適用例について述べていきます。

定義とその解説

キルヒホッフの電圧則 (第 2 法則)の定義

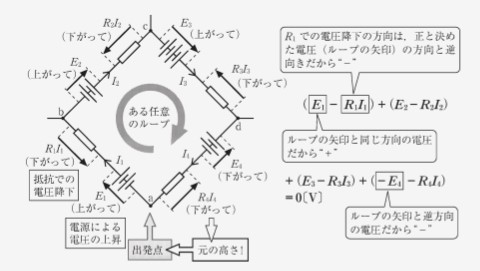
電気回路の中で任意のループを考えたとき、そのループに沿って、1 方向に 1 周りしたときの電圧の総和はゼロである。

数式で表すと以下のようになります。これをあるループにおける閉路方程式と呼びます。なお、$E$は電位、$R$は抵抗、$I$は電流とします。

$$\sum_{k=1}^{n} R_k I_k = \sum_{i=1}^{m} E_i$$

こちらも、基本的にはループの中でのエネルギー保存を意味していますので、以下のように言い換えることができます。

キルヒホッフの電圧則 (第 2 法則)の言い換え

電気回路の中での任意のループ内部では、電源による電圧の上昇分と、抵抗での電圧降下分の総和はゼロである。

使い方

キルヒホッフの電圧則 (第 2 法則)を用いて各節点の電位を求める手順は、次の通りです。
教科書の P.25 には 1～4 までのステップが示されていますが、5 と 6 も追加すると手順が明確になると思います。

1. 各枝路に流れる電流 $I_1, I_2$ などを仮定する
2. 閉路 (ループ) をとり、ループの向き (正とする電圧の方向) を決める
3. ループの向きに、その閉路の電圧の方向を考慮して足し合わせる
4. 「足した式 = 0」 という形の閉路方程式を立てる
5. 立てられた閉路方程式の数が、各枝路に必ず一度は閉路が通過する最小の閉路の数となるまで、3 を繰り返す
6. 立てた閉路方程式を電流について解く

閉路方程式をすべての枝路、つまり仮定した電流について、立てることがポイントです。
また、閉路方程式は、着目しているループ以外の部分を無視できる点もポイントです。

適用例

教科書 P.31 の例題 2.1 をキルヒホッフの電圧則を使って問いてみます。
「次の回路の接点の電圧$V_1, V_2$をキルヒホッフの電圧則を用いて求めよ。」

教科書 P.26 の回路をキルヒホッフの電圧則を使って問いてみます。
「次の回路に流れる電流$I_1, I_2$をキルヒホッフの電圧則を用いて求めよ。」

演習問題 2.1

教科書 P.35 の演習問題 2.1 をキルヒホッフの電圧則を使って問いてみましょう。

キルヒホッフの電圧則と電流則の使い分け

例題 2.1 は、電圧則と電流則のどちらを使っても、電流と電圧を求めることができます。
ここでは、両者の使い分けについて述べていきます。

使い分けの判断基準

1. 各枝路の抵抗に流れる電流分布を求めたいときは、電圧則で閉路方程式を作る。
2. 電流分布が仮定できないときや、節点の電圧を求めたいときは、電流則で節点方程式を作る。

また、節点の数と閉路の数のどちらか少ないほうの解法を選ぶという基準もあります。

電流則の場合は、節点に入出力するすべての電流を考えなくてはいけません。
しかし、電圧則の場合は、ループに含まれないものは無視しても問題ありません。
そのため、電圧則はループのみに着目すればよいため、シンプルに回路を解析できる場合が多いです。

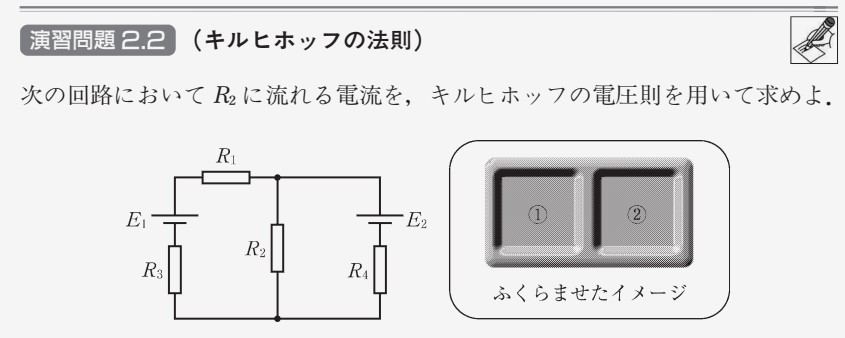
演習問題 2.2

演習問題 2.2 をやってみましょう

シミュレーション結果

追加問題

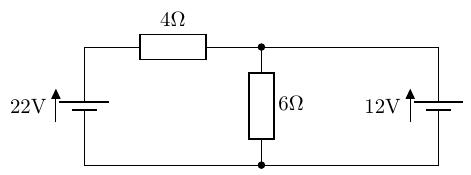
以下の回路の、各抵抗を流れる電流を求めよ。

シミュレーション結果

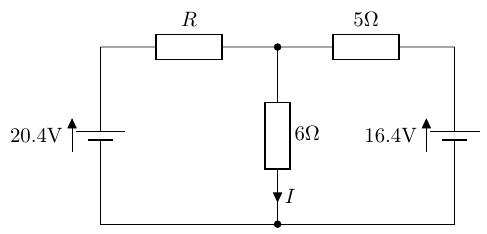
以下の回路の、6[$\Omega$]の抵抗を流れる電流$I$が 2.4[A]となるような、抵抗$R$の値を求めよ。

シミュレーション結果