第8回 ここまでの練習問題
ここまで、直流回路の解析に関する方法が一通り終わりました。 まとめとして、以下の問題を解いてみましょう :)
問題1 合成抵抗、分圧・分流
図の回路の抵抗の両端の電圧が 6[V]、電流が 1 であった。抵抗を求めよ。
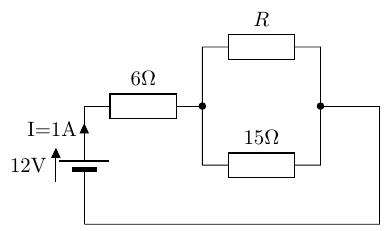
答え: R=10[]
問題2 キルヒホッフの定理
次の回路に流れる電流を求めよ。
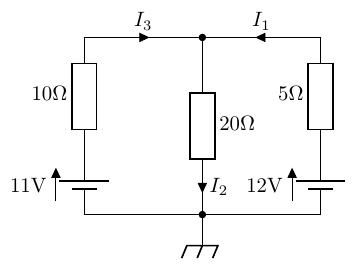
答え: 0.4[A], 0.5[A], 0.1[A]
問題3 電流源と電圧源
図の回路において、電圧源に流れる電流と、に流れる電流を求めよ。
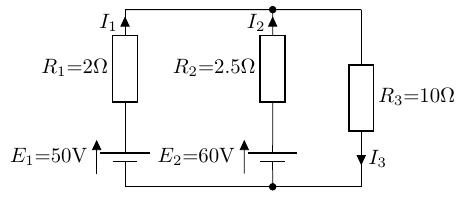
答え: 0.5[A], 4.4[A], 4.9[A]
問題4 重ねの理
重ね合わせの理を使って、次の回路の電流を求めよ。
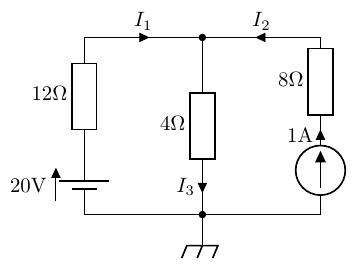
答え: 1[A], 1[A], 2[A]
問題5 テブナンの定理、ノートンの定理
回路図の ab 間の抵抗 4[]に流れる電流を求めよ。
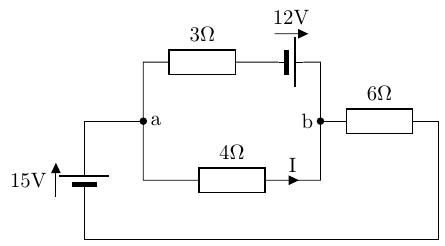
答え: I = 0.5[A]
問題6 最大電力の定理
以下の回路で、R をいくつにしたときに電源 E=10V から最大の電力が供給されるか?またそのときの R で消費される電力はいくらか?
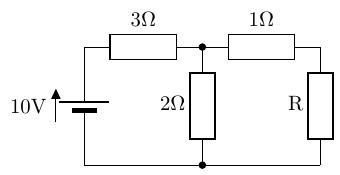
答え: R = 2.2[], [W]