第3回 オームの法則と電力

電気回路の用語

今回は、電気回路を構成するもっとも基礎的な用語について定義と解説を行います。
これらの用語は、直流回路と交流回路のどちらでも頻出の用語ですので、確実に理解してください。

電流 (Electric Current) とその単位

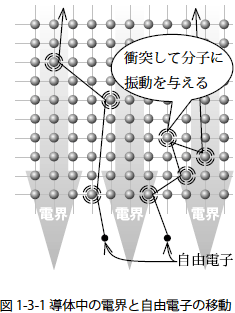
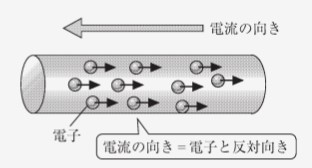
• 電流の定義：電流は、電荷を持つ自由電子の流れのことです。また、電流の流れの向きは、負電荷の移動方向と反対向きとします。
  

• 電流の単位 [A] (ampere, アンペア) の定義：1[A]とは、ある断面に 1[sec] (seconds, 秒)に、1[C] (coulomb, クーロン) の電荷が流れる密度のことです。

これらの定義から、電流 $I$[A]、電荷 $Q$[C]、時間 $t$[sec]の間には、以下の関係式が成り立ちます。

$I [A] = {Q} [C] \div {t} [sec]$

電圧 (Voltage) とその単位

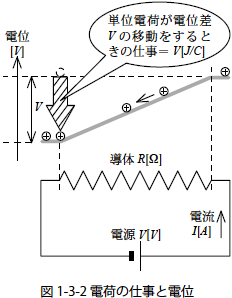
• 電圧の定義：電圧は、2 点間の電位の差のこと。

• 電圧の単位 [V] (voltage, ボルト) の定義：1[V]とは、1 [A]の電流が流れる物体の 2 点間で消費される電力が 1 [W] (watt, ワット)であるときの、その 2 点間の電圧の差

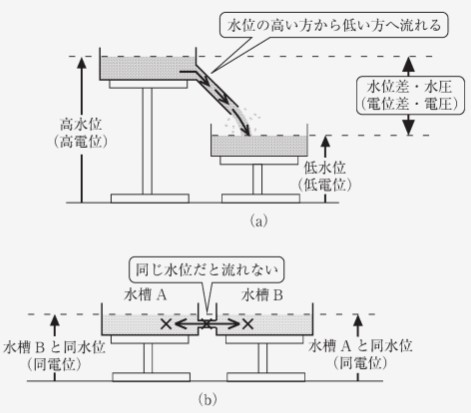
2 点間の電位に差 (電位差) があれば、電位の高いほうから電位の低いほうに電流が流れます。

また、電圧は電位の差と定義されるので、その差の大きさはどこを基準とするのかで値が変わってきます。基準点 (0V) を示す回路記号に、以下の接地点があります。

接地点の回路記号

これらの定義から、電圧 $V$[V]、電力 $P$[W]、電流 $I$[A]の間には、以下の関係式が成り立ちます。

$V [V] = {P} [W] \div {I} [A]$

電気抵抗 (Electrical Resistance) とその単位

• 電気抵抗の定義：電気抵抗は、電流の流れにくさのこと。

• 電気抵抗の単位 [$\Omega$] (Ohm, オーム) の定義：1[$\Omega$]とは、2 点間に印加された 1[V]の電位差が、この物体に 1 [A]の電流を生じさせるとき、その 2 点間に存在する電気抵抗のこと。

これらの定義から、電流 $I$[A]、電圧 $V$[V]、抵抗 $R$[$\Omega$]の間には、以下の関係式が成り立ちます。この関係式をオームの法則と呼びます。

$I [A] = {V} [V] \div {R} [\Omega]$

電力 (Electric Power) とその単位

• 電力の定義：電力とは、電気エネルギーが単位時間あたりに行う仕事率のこと。

• 電力の単位 [W] (watt, ワット) の定義：1[W]とは、1[sec]に 1[J] (jules, ジュール) の仕事をする電力のこと。

これらの定義から、電力$P$[W]、電力量$W$[J]、時間$t$[sec]には以下の関係式が成り立ちます。

$P [W] = {W} [J] \div {t} [sec]$

また、電流と電圧の定義より、以下の関係式も成り立ちます。（導出してみましょう）

$P [W] = {I} [A] \times {V} [V]$

オームの法則 (Ohm's law)

オームの法則は$I [A] = {V} [V] \div {R} [\Omega]$ ですが、この法則のこれの意味するところは以下の 2 つであり、そのイメージは以下のようなものです。

• 意味するところ

  1. 電流の大きさは、電圧の大きさに比例する
  2. 電流の大きさは、抵抗の大きさに反比例する

• イメージ
  

教科書の演習問題 1.1 ~ 1.3

直流回路とその構成

ここでは、基礎的な電気回路として直流回路における抵抗の直列接続や並列接続について考えていきます。

回路記号

本講義で扱う回路記号には以下のようなものがあります。1997 年に新 JIS 規格で新しい回路記号になりましが、古い記号もよく見かけますので、覚えておくと便利です。

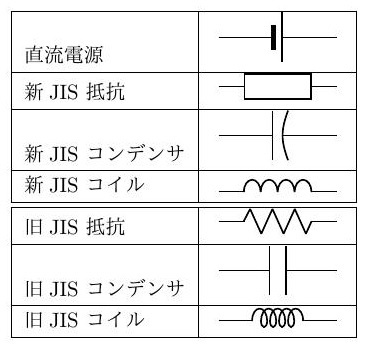
本講義で扱う回路記号

直流回路とは

• 直流電流の定義：直流電流とは、流れる電流の大きさが一定であり、その流れる方向も常に一方向である電流のこと。

  
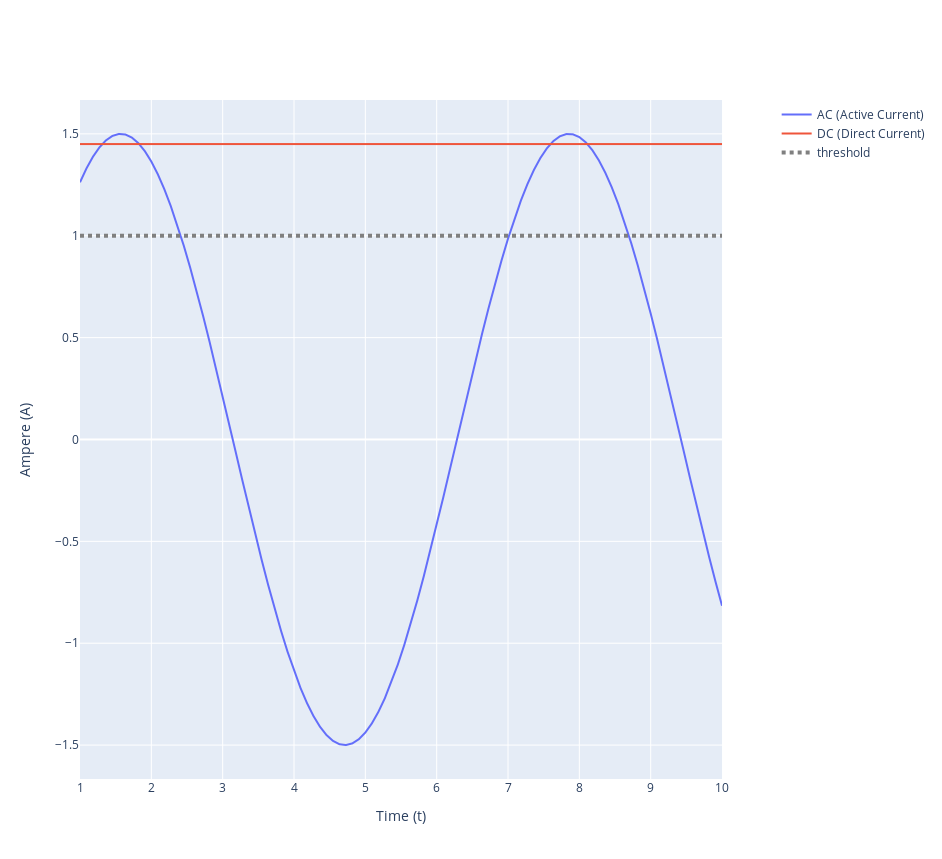
  直流電流と交流電流の電流のとき系列変化。直流電源は電流の大きさが一緒だが、交流電源は電流の大きさがときどき刻々と変化する。

• 直流回路の定義：直流回路とは、直流電流が流れる電気回路のこと。

• 直流電源の定義：直流電源とは、直流電流を流せる電源のこと。

  直流電源は以下の回路記号で表される。$v_1, i_1$は、それぞれ電圧と電流。もっとも一般的な直流電源は、乾電池。モバイルバッテリーも直流電源の 1 つ。

  
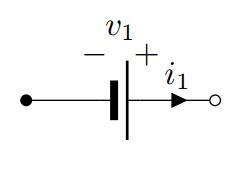
  直列電源の回路記号

抵抗の直列接続

以下の図のように、直流回路に抵抗を直列に接続する電気回路を考えます。

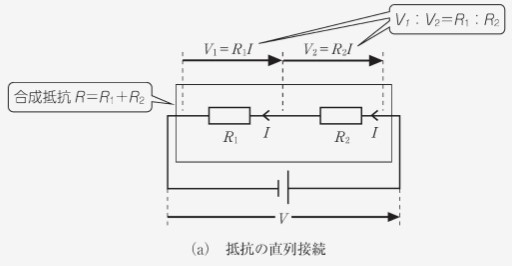
(a) 抵抗の直列接続

このとき、2 つの抵抗$R_1$と$R_2$には、同一の電流$I$が流れます。
複数の抵抗を接続した場合、1 つの大きな抵抗と考えることができ、それを合成抵抗と呼びます。
この考え方は、直列接続か並列接続かによりませんが、合成抵抗の計算のし方が変わります。

直列接続の場合、合成抵抗はすべての抵抗の総和になります。
また、オームの法則を用いることで、各抵抗にかかる電圧が算出できます。
具体的には、抵抗にかかる電圧の大きさは、その抵抗の大きさに比例します。 電圧を分配するとも考えられるので、分圧と呼ばれます。

抵抗の並列接続

以下の図のように、直流回路に抵抗を並列に接続する電気回路を考えます。

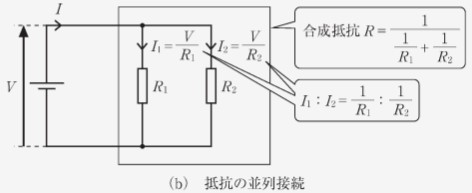
(b) 抵抗の並列接続

このとき、2 つの抵抗$R_1$と$R_2$には、同一の電圧$V$が付与されます。
付与される電圧は、オームの法則より以下のように算出できます。

$I = I_1 + I_2 = \frac{V}{R_1} + \frac{V}{R_2} = (\frac{1}{R_1} + \frac{1}{R_2})V$

$(\frac{1}{R_1} + \frac{1}{R_2})$の部分は、合成抵抗$R$の逆数にあたり、これを展開すると、以下のようになります。

$R = \frac{1}{(\frac{1}{R_1} + \frac{1}{R_2})}$

並列接続の場合、合成抵抗はそれぞれの抵抗の逆数の総和になります。
抵抗にかかる電流の大きさは、その抵抗の大きさに比例します。
電流を分配するとも考えられるので、分流と呼ばれます。

教科書の演習問題 1.4 ~ 1.9

演習問題 1.7 の答えの$I_2$が間違っているようです。分子は$R_3$ではなく$R_2$です。正確には以下の値になります

• 誤: $I_{3} = \frac{ \mathbf{R_3} }{R_{1}R_{2} + R_{2}R_{3} + R_{3}R_{1}} E$

• 正: $I_{3} = \frac{ \mathbf{R_2} }{R_{1}R_{2} + R_{2}R_{3} + R_{3}R_{1}} E$

演習問題追加

1. 以下に示す回路において、端子 C-E 間の合成抵抗を求めよ。
   

---

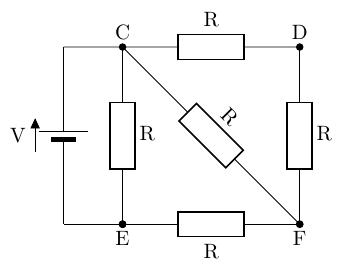
電力と電力量

ここからは、これまでに定義した電気回路の用語を元に、電力 (Electric power) や電力量 (Electric energy) 、ジュール熱 (Joule heat) について述べていきます。 電力は仕事率、電力量は仕事の量、ジュール熱は熱エネルギーを示す値です。 電力と電力量はそれほど難しい概念ではありませんが、電力量とジュール熱の関係は少し分かりにくいかもしれません。

なお、教科書では、P.99 第 5 章「電力と電力量」にあたる内容です。

ポイントは以下のとおりです。

• 仕事率とは、単位時間あたりの仕事の能力

• 仕事量とは、ある時間で行った仕事の総量

• 電力とは、単位時間あたりに電気が行う仕事率

• 電力量とは、ある時間で電気が行った仕事量

• 電気が行う仕事とは、電荷をとある電位差だけ動かすこと

電力

電力は、平たく言うと、電圧と電流が単位時間あたりに行う仕事のことです。

• 電力の定義: 電力とは、ある電流とある電圧が単位時間当たりに行う仕事率のこと。
• 電力の単位 [W] (watt, ワット) の定義: $P$[W]とは、電圧$V$と電流$I$の積となる。

よって、電力$P$[W]と電圧$V$と電流$I$には以下の関係が成り立ちます。
$P = IV = I^2 R = \frac{V^2}{R}$

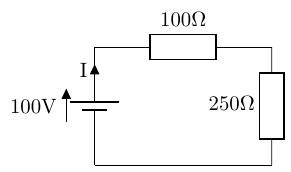
演習問題 5.1

定格 100V で 100W の電球と、定格 100V で 40W の電球を直列につないで 100V の電圧源につないだとき、どちらの電球の方が明るくなるか？ （2 つの電球を直列につないで 100V をかける→電源電圧のぶん圧により、それぞれの電球にかかる電圧は 100V ではなくなる。分圧については、別の回で説明します。）

電力量

電力は単位時間あたりの仕事量ですので、ある時間での仕事全体を示す量として電力量を定義します。単位は[W $\times$ s]です。

• 電力量の定義: 電力量とは、ある電流がある時間に行った仕事全体のこと。
• 電力量の単位 $W$[W$\cdot$s] (work, 仕事) の定義: $W$[W$\cdot$s]とは、仕事$P$[J]をある時間$t$[sec]にわたって行ったときの仕事量のこと。

よって、電力量 $W$[W $\cdot$ s]と電力$P$[W]、時間$t$[sec]電圧$V$[V]と電流$I$[A]には以下の関係が成り立ちます。
$W = P \times t = IVt$

電力量の単位 W の定義は時間の単位を秒[sec]としましたが、現実世界では単位として時間[hour]と[kW]を使い[kWh]として表すことがよく見受けられます。たとえば、東京電力の電気代は、1[kW$\cdot$h]で計算され、だいたい 20 円くらいです。単位をジュール熱[J]とすることもできますが、電気によるエネルギーを示す場合には、こちらを使用することが一般的です。

演習問題 5.2（改）

500W のドライヤーを 20 分間使うのと、1200W のドライヤーを 8 分間使うのとでは、どちらが何円くらい経済的か？20 円/[kW$\cdot$h]で計算せよ。

ジュール熱

ジュール熱は、導体に電流が流れるときに発生する熱です。これを電流が行った仕事の結果として見ることで、電力量と熱を結び付けます。

• ジュール熱の定義: ジュール熱は、ある抵抗を持つ導体に電流を流したときに生じる発熱であるジュール効果によって発生する熱エネルギーのこと。

• ジュール熱の単位[J]の定義: あるジュール熱$Q$[J]とは、ある電圧 $V$[V] が印加された抵抗に電流$I$[A] を $t$[s] 間だけ流したときの熱量

よって、ジュール熱$Q$[J]、電圧$V$[V]、電流$I$[A]、時間$t$[sec]には以下の関係式が成り立ちます。
$Q = I V t$
この式にオームの法則を適用すると、次式が導けます。
$Q = I V t = R I^2 t = \frac{V^2}{R}t$

つまり、ジュール熱の量は、抵抗 $R$ と電流 $I$ の二乗の積に比例します。イギリスの物理学者、ジェームズ・ジュールが実験によって発見した物理法則で、ジュールの法則と呼ばれています。

電力量とジュール熱の概念的な説明

ここでは、電力量とジュール熱が同値であることを概念的に説明します。物理的な定義や電磁気学的な定義はスキップしていますが、イメージがつかめればと良いと思います。細かい話は、電気磁気学の本などを読んでみてください。

出典：胴体中の電解と自由電子の移動 - 大川電子設計製作

電気回路中では、電源が電圧を印加することによって、ある電位差が発生します。 発生した電位差によって電磁気力が発生し、回路中の自由電子はその電磁気力を受けて移動します。 これは、「電源は、自由電子がある電位差の 2 点間を動かす量だけの仕事をした」と考えることができます。

これを式で表すと以下のようになり、電力量が導けます。なお、$W$[C $\times$ V]を電力量、自由電子の電荷を$q$[C]、電位差を$V$[V]とします。
$W = q \times V$

ところで、自由電子が物体の中を動くとき、自由電子は導体を構成する分子に衝突しながら動きます。このとき、衝突した自由電子は運動エネルギーを失って減速し、衝突された分子は力学的なエネルギーを受けて振動します。分子が振動して発生した熱をジュール熱と言います。（すべてのエネルギーが熱振動に変わったとします。） つまり、「自由電子が動いて、ジュール熱を発生させた」と言えます。

上記の 2 つの事象は自由電子によりつながっており、「電源が行った仕事量は、発生したジュール熱として消費された」と言えます。
これを式で表すと以下のようになり、仕事量はジュール熱と言い換えられることになります。なお、$Q$[J]をジュール熱、$W$[$C \times V$]自由電子の電荷を$q$[C]、電位差を$V$[V]とします。
$`Q = W = q \times V$

出典：ジュール熱 - 大川電子設計製作

なお、電力量への変換には、電流と電荷の関係式 $I = \frac{q}{t}$を用います。
$Q = q \times V = I t V$

単位変換

電力の単位は、以下のように相互変換できます。
[W] = [J]$\div$[s] = [A]$\times$[V]

電力量の単位は、以下のように相互変換できます。
[J] = [W]$\times$[s] = [A]$\times$[V]$\times$[s] = $[A]^2 \times$[Ω]$\times$[s] = $[V]^2\times$[s]$\div$[Ω]

身近な例

電力や電力量は身近な存在です。 以下にいろいろな電力や電力量の値を列挙します。 それぞれの数字を比較することで、感覚を身に着けてほしいと思います。

家電製品いろいろ

• 家庭の電流: 30,40,50A
• 家庭の消費電力/月: 200~500kWh くらい
• 家庭用 LED: 3～8W
• 冷蔵庫(年間消費電力量): 300kWh 程度(一日 1kWh 程度)
• エアコン: 3kWh 程度

車いろいろ

• 電気自動車: Tesla Model 3 (普通のモデル)

  • バッテリー容量: 50 kWh (スタンダードレンジ)
  • バッテリー電圧: 400V
  • バッテリー定格/最大電流: ???/125A 程度? ($P = I \times V, 50kWh = I \times 400, I = 125A$)
  • モータ定格/最高出力: ???/202kW

• 電気自動車: Tesla Model S (高いモデル)

  • バッテリー容量: 100 kWh (スタンダードレンジ)
  • バッテリー電圧: 400V
  • バッテリー定格/最大電流: ???/250A 程度? ($100 \div 400, I = 250A$)
  • モータ定格/最高出力: ???/451kW

• 電気自動車: 日産自動車リーフ

  • バッテリー容量: 62kWh
  • バッテリー電圧: 350V
  • バッテリー定格/最大電流: 60/177A 程度? ($62 \div 350$)
  • モータ定格/最大出力: 70/80kW

• ハイブリッドカー(PHEV): トヨタ プリウス

  • バッテリー容量: 8.8kWh
  • バッテリー電圧: 330V
  • バッテリー定格/最大電流: 75/???A
  • モータ定格/最大出力: 18/60kW

• 電動自転車 Panasonic VIVI TX

  • バッテリー容量: 159Wh
  • バッテリー電圧: 25.2V
  • バッテリー定格/最大電流: 6.6/6.3A 程度? ($159 \div 25.2$)
  • モータ定格/最大出力: 250/???W

コンピュータいろいろ

• スーパーコンピュータ: 富岳

  • 最大消費電力: 30MW

• ノート PC: Lenovo ThinkPad X1 Carbon 2021

  • バッテリー容量: 57Wh
  • バッテリー電圧: 12V
  • バッテリー定格電流: 5A ($57 \div 12$)

• スマートフォン: Sony Xperia 1

  • バッテリー容量: 4500mAh ($4.5Ah \times 3.8 = 17.1Wh$)
  • バッテリー電圧: 3.8V
  • バッテリー定格電流: 1A 程度

最大電力の法則

とある回路の電圧源(理想電圧源と内部抵抗)から、回路に供給する電力、つまり、抵抗が消費する電力が最大になるためにはどうすればよいか考えてみます。

以下の簡単な回路で考えてみます。内部抵抗 r と電圧源 E、それにつながった抵抗 R、の 3 つがつながった回路です。

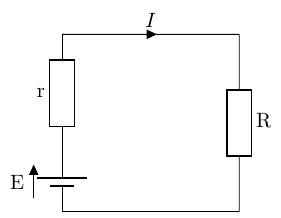
回路に流れる電流は、以下のようになります。
$I = \frac{E}{r + R}$

抵抗 R での消費電力$P$[W]は、以下のように抵抗 R のみが変数となります。
$P = I^2 \cdot R = (\frac{E}{r + R})^2 \cdot R = \frac{R}{(r+R)^2} E^2$

抵抗 R で消費される電力が最大になる条件を考えてみます。
そのためには、P の極限を与える R の値を求めます。つまり、P を R で微分し、それが零となる R の値を求めれば良い、ということになります。

$\frac{\partial P}{\partial R} = \frac{\partial}{\partial R} {\frac{E^2 R}{(r+R)^2}} = E^2 \frac{(r+R)^2 - R \times 2(r+R)}{(r+R)^4} = E^2 \frac{r^2 - R^2}{(r+R)^4} = E^2 \frac{(r+R)(r-R)}{(r+R)^4} = E^2 \frac{(r-R)}{(r+R)^3}$

R	R < r	R = r	R > r
$\frac{\partial P}{\partial R}$	正	0	負
P	増加	最大値	減少

以上より、$R = r$のとき、最大の電流が流れることとなります。 これを最大電力の法則と呼びます。

たとえば、E=20[V]で内部抵抗 r = 1,2,3,4,5[$\Omega$]としたとき、抵抗 R を変化させたときの消費電力 P[W]をプロットしたものが、以下のグラフになります。それぞれ、r=R のときに消費電力 P が最大になっているのが見て取れます。

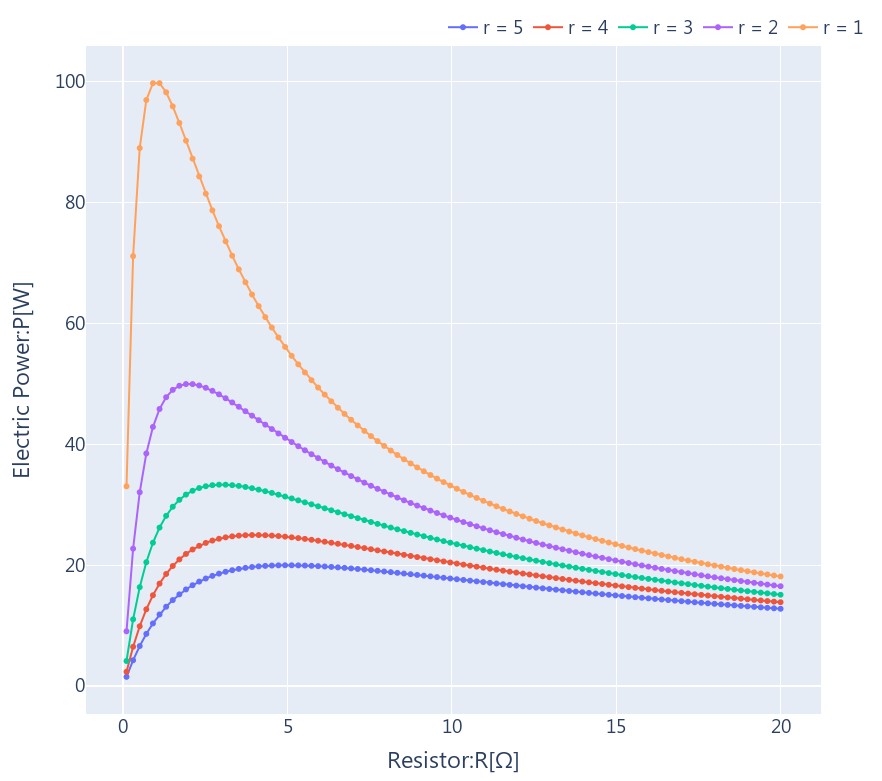
また、最大消費電力は$R = r$として、以下のように計算できます。
$P = E^2 \frac{r}{(r+R)^2} = \frac{r}{(r+r)^2}E^2 = \frac{r}{4r^2}E^2 = \frac{E^2}{4r}$

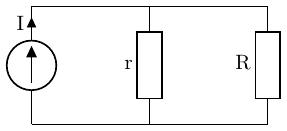
演習問題 5.3

次の回路において、抵抗 R で消費される電力を求め、さらにその最大値を求めよ。

付録

定義、公理、定理とは

• 定義 (definition)は、ある言葉やある概念を、ほかの言葉や概念と明確に区別できるように指定することです。その言葉が何を意味するかを明確化する目的で、本講義では利用します。言葉の定義は、覚える必要があります。

• 公理 (axiom)は、自明であるため、特に理由なく無条件で正しいと仮定する事柄や前提条件のことです。公理は、無条件で正しいとして扱うため、もしかすると間違っているかもしれません。

• 定理 (teorem)は、公理と定義を用いて導きだされ、正しいことが証明できる事項のことです。もしも、公理が間違っている場合、定理も間違ったものが導かれます。