第6回 重ねの理
今回は、重ねの理 (superposition theorem) について解説し、使い方を説明します。 前回の電流源と電圧源は、両者を等価変換して回路を変換することで、複雑な回路を簡単に解析するためのものでした。 重ねの理を用いることで、複雑な回路を複数の簡単な回路として扱うことができます。
重ねの理
定理の説明
重ねの理とは、以下の公理のことを言います。
重ねの理
回路中に複数の電源が存在する場合、ある枝路を流れる電流やある節点にかかる電圧は、それぞれの電源が単独に存在する場合に流れる電流や電圧の総和で与えられる。
言い換えると、回路中に複数の電源が存在する場合、回路の枝路に流れる電流や節点の電圧は、各電源が回路に単独で存在したときに、その枝路に流れる電流や節点にかかる電圧を合計したものとなります。
細かい話
重ねの理は定理であり、定義ではありません。 定理は、公理と定義を用いて導きだされ、正しいことが証明できる事項のことです。 重ねの理の導出に用いられる定義はオームの法則などですが、公理は「電気回路の線形性」です。
電気回路の線形性とは、「回路にある電圧を印加したときに、その大きさに比例した電流が流れる性質」のことです。 つまり、n 倍の電圧を掛けると、n 倍の電流が流れる性質です。 この性質は、電気回路が抵抗やコンダクタ、インダクタ、電圧源、電流源のような線形回路素子のみで構成される場合に成り立ちます。 本講義で扱う回路素子はすべて線形性を持ち、線形回路素子に分類されます。 詳細については、参考書『例題と演習で学ぶ電気回路』の"3.3 電気回路の線形性"を読んでみてください。
なお、トランジスタやダイオードは線形回路素子ではなく非線形回路素子です。 これは、ダイオードは印加する電圧がある閾値以上になると急激に電流が増えるため、電圧と電流の比例関係が成り立ちません。 つまり、ダイオードを含む電子回路は、重ねの理を適用できません。
使い方
電圧源を持つもの
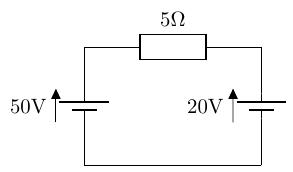
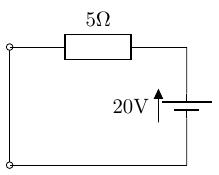
以下の非常に簡単な回路の抵抗に流れる電流を考えてみます。
重ねの理を使わないで計算すると、抵抗にかかる電圧はですので、となります。
重ねの理を使って、各電源が回路に単独で存在した場合を考えます。
電圧源を無視する場合、考慮しないほうの電圧源は、単なる配線として短絡することがポイントです。
これは、この講義の範囲内では電圧源は理想電圧源であり、抵抗が零である内部抵抗と電圧源に分解できるためです。
- 左側の電源のみを考えると、抵抗に流れる電流は、となります。
- 右側の電源のみを考えると、抵抗に流れる電流は、となります。※電流が流れる方向は、左側の電源のみを考えた回路とは逆と仮定。
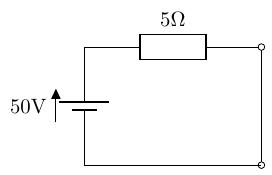
左側の電源のみ 右側の電源のみ
重ねの理を用いて、両者を足し合わせると、と求めることができます。
シミュレーション結果
電流源を持つもの
以下の非常に簡単な回路の抵抗に流れる電流を考えてみます。
重ねの理を使わないで計算すると、抵抗にかかる電流はとなります。
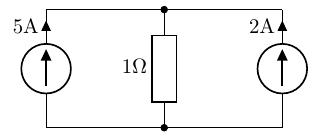
重ねの理を使って、各電流源が回路に単独で存在した場合を考えます。
電流源を無視する場合、考慮しないほうの電流源は開放することがポイントです。
これは、電流源は理想電流源であり、抵抗が無限大である内部抵抗と電流源に分解できるためです。
- 左側の電源のみを考えると、抵抗に流れる電流は、となります。
- 右側の電源のみを考えると、抵抗に流れる電流は、となります。
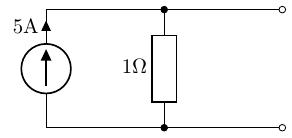
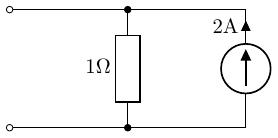
左側の電流源のみ 右側の電流源のみ
重ねの理を用いて、両者を足し合わせると、と求めることができます。
シミュレーション結果
適用例
ここでは、もう少し複雑な回路に重ねの理を適用してみます。
簡単な回路
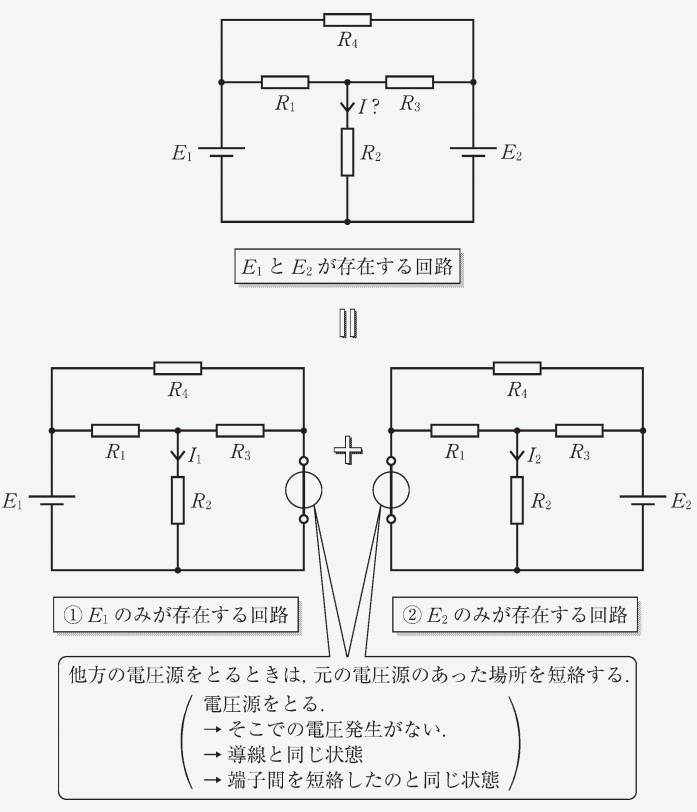
最初に挙げた、教科書 P.62 の上の回路を考えてみましょう。 この回路の電流を求める場合、重ねの理を利用することで、2 つの電圧源それぞれがもととなる電流の足し合わせとして考えることができます。 なお、この回路では電流源と電圧源の等価変換は適用できません。
この回路を重ねの理を用いて、とのみが存在する回路①と②に分解します。

図左下の回路①がの部分に流す電流は、合成抵抗と分流の法則を用いて計算すると以下のようになります。
また、図右下の回路②は、がの部分に流す電流は、同様に計算すると以下のようになります。
よって、は重ねの理より、以下のようになります。
としたときのシミュレーション結果
電圧源と電流源の混ざった回路
教科書 P.64 の回路の抵抗に流れる電流を求めてみましょう。
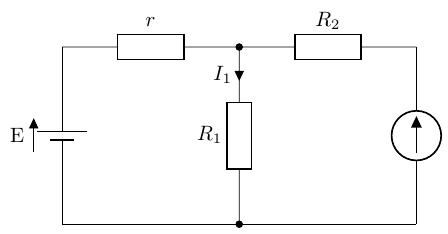
-
左側の電圧源のみを考えると、抵抗に流れる電流はオームの法則より、となります。
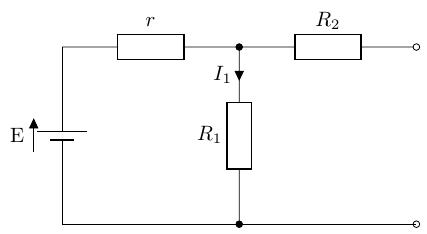
-
右側の電流源のみを考えると、抵抗に流れる電流は分流の法則より、となります。
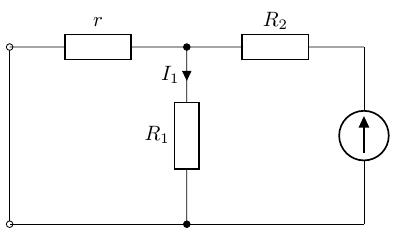
よって、電流は重ねの理より、以下の形となります。
としたときのシミュレーション結果
演習問題
演習問題 3.5
教科書 P.66 の演習問題 3.5 をやってみましょう。
次の回路において抵抗に流れる電流を求めよ。
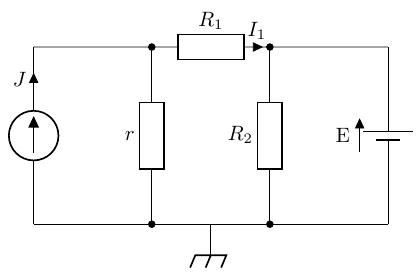
としたときのシミュレーション結果
追加問題
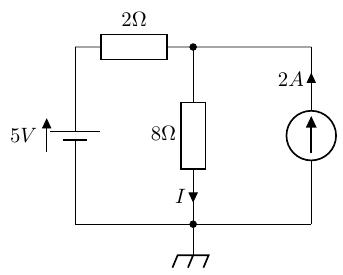
以下の回路において、8[]の抵抗を流れる電流を、重ねの理を用いて求めよ。