第7回 テブナンの定理とノートンの定理
今回は、テブナンの定理 (Thevenin's theorem)とノートンの定理 (Norton's theorem)について取り扱います。 テブナンの定理は複雑な回路のある枝路の電流を求めるのに便利な定理で、ノートンの定理は複雑な回路のある枝路の電圧を求めるのに便利な定理です。 また、テブナンの定理とノートンの定理は双対関係にあります。
テブナンの定理
テブナンの定理は、キルヒホッフの法則より簡単に、ある枝路に流れる電流の大きさを求める定理です。
定理の説明
テブナンの定理を言葉で表すと、以下のようになります。
テブナンの定理
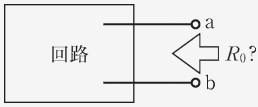
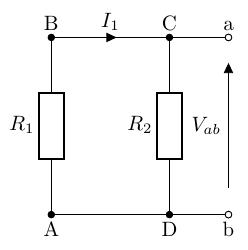
ある回路網から出ている 2 つの端子間を開放したときに現れる電圧(開放電圧1)をとする。また、回路網中の電源を取り去ったとき、この 2 つの端子からみた回路網の内部の合成抵抗をとする。この端子間に抵抗をつないだとき、この抵抗に流れる電流は、次式で与えられる。
この定理のイメージは、以下のようなものになります。
とある回路の抵抗に流れる電流を求めたいとき、その抵抗以外の部分の回路を抵抗と開放電圧の 2 つからなる等価な電圧源に変換し、そこからオームの法則で電流を求めます。また、端子 間に掛かる電流を求めたいので、2 点間を開放します。
図の枠線で囲われた部分は本来は複雑な回路ですが、この部分をこれまで学んだ法則や定理を使って等価な電圧源に変換します。
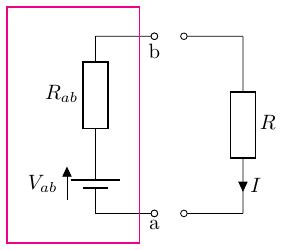
教科書の P.70 では、なぜこの定理が成り立つかが説明されています。
使い方
ここでは、テブナンの定理を利用する際の手順について述べます。 ポイントは、端子間を開放し、そこに掛かる開放電圧を求めることです。 また、これまで学んだ定理などを利用して、端子以外の部分を抵抗と開放電圧の 2 つからなる等価な電圧源に変換する点も重要です。
具体的な手順は以下のとおりです。
- 目的:以下に示す、とある複雑な回路の枝路の抵抗に流れる電流を求めたい。
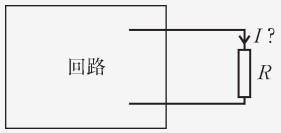
-
求めたい電流が流れている枝路の抵抗を取り除き、その部分を端子とします。(この時点では、回路を開放したわけではありません。)
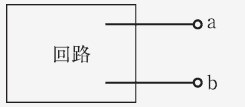
-
間を開放し、端子間の開放電圧を求めます。このとき、これまで学んだ定理などを利用します。
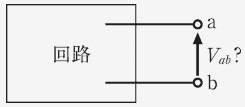
-
端子 間は短絡したままで、端子間から見た回路の合成抵抗 、もしくは、コンダクタンスを求めます。このとき、これまで学んだ定理などを利用します。
-
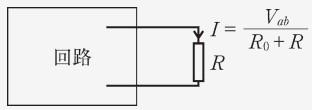
最後に、求めた開放電圧と抵抗より、端子 間につながれている抵抗が に流れる電流 は、以下の式から計算できます。なお、枝路に抵抗がないときは とします。
適用例
電圧源を持つもの
以下の電圧源が 2 つ並列接続された回路を考えてみます。
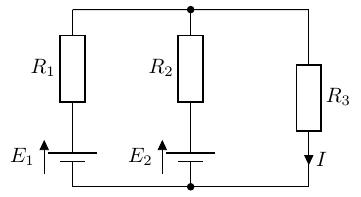
この抵抗に流れる電流を、テブナンの定理を用いて求めよ。キルヒホッフの法則でも計算ができますが、テブナンの定理を用いてみます。
-
求めたい電流が流れている枝路の抵抗を取り除き、その部分を端子とします。また、問題を解きやすくするために、開放電圧などを定義します。
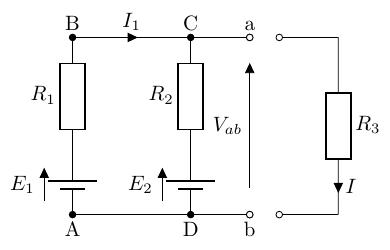
-
間は開放し、端子 間の開放電圧を求めます。この例では、左側の回路についてキルヒホッフの開放電圧則を適用します。
- 左側の閉回路の方程式:
- よって、
- 点に掛かる電圧はと同一ですので、開放電圧は以下のようになります。
-
端子 間は短絡したままで、端子 間から見た回路網の合成抵抗 を求めます。このとき、電圧源を短絡します。
短絡した結果、合成抵抗は以下の形で与えられます。
-
最後に抵抗に流れる電流は、求めたと抵抗とテブナンの定理より以下のように計算できます。 つまり、テブナンの定理: に、ここまで求めたとを代入します。
電流源を持つもの
以下の回路の 4の抵抗に流れる電流を求めます。
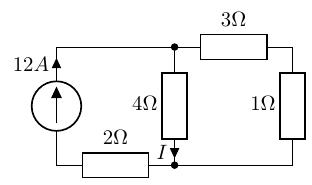 分流の法則よりと求められますが、テブナンの定理を用いてみます。
分流の法則よりと求められますが、テブナンの定理を用いてみます。
-
求めたい電流が流れている枝路の抵抗を取り除き、その部分を端子と定義します。
-
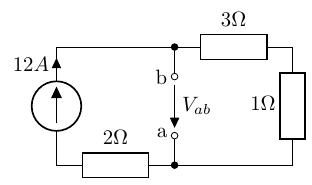
端子 間は開放し、 間の開放電圧を求めます。
- 電流源にかかっている電圧:
- 分圧の法則より、
-
端子 間から見た回路網の合成抵抗 を求めます。このとき、回路中の電流源は開放します。 その結果、右側の閉回路だけが残り、単なる直列の合成抵抗となります。
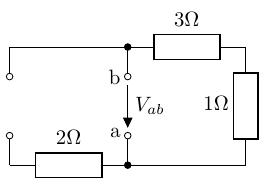
-
4の抵抗に流れる電流は、求めた開放電圧と抵抗とテブナンの定理より以下のように計算できます。
演習問題
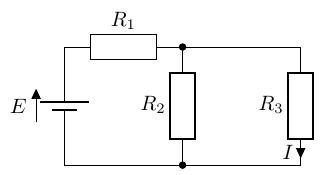
例題 4.2
次の回路でに流れる電流を求めよ。
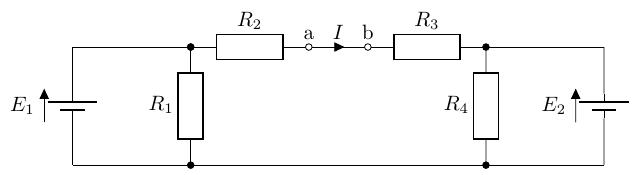
例題 4.3
次の回路で端子 間に流れる電流を求めよ。
ノートンの定理
ノートンの定理は、キルヒホッフの法則より簡単に、ある枝路に流れる電圧の大きさを求める定理です。 テブナンの定理の双対になりますので、雰囲気は似ています。
定理の説明
ノートンの定理を言葉で表すと、以下のようになります。
ノートンの定理
ある回路網から出ている 2 つの端子間を短絡したときに流れる電流(短絡電流2)をとする。
また回路網中の電源を取り去ったとき、この 2 つの端子から見た回路網の内部抵抗をとする。
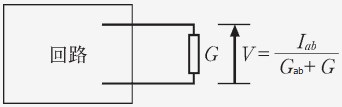
この端子間に抵抗をつないだとき、この抵抗の両端に発生する電圧は次式で与えられる。
なお、をととの合成抵抗、とのコンダクタンスをそれぞれととする。
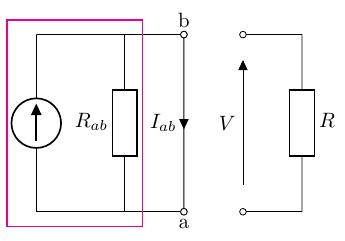
この定理のイメージは、以下のようなものになります。
とある回路の抵抗に掛かる電圧を求めたいとき、その抵抗以外の部分の回路を抵抗と短絡電流の 2 つからなる等価な電流源に変換し、そこからオームの法則で電圧を求めます。また、端子 間に掛かる電圧を求めたいので、2 点間を短絡します。
図の枠線で囲われた部分は本来は複雑な回路ですが、この部分をこれまで学んだ法則や定理を使って等価な電流源に変換します。
教科書の P.80 では、なぜこの定理が成り立つかが説明されています。
使い方
ここでは、ノートンの定理を利用する際の手順について述べます。 ポイントは、端子間を短絡し、そこに流れる短絡電流を求めることです。 また、これまで学んだ定理などを利用して、端子以外の部分を抵抗と短絡電流の 2 つからなる等価な電流源に変換する点も重要です。
- 目的:以下に示す、とある複雑な回路の枝路の抵抗に掛かる電圧$``$を求めたい。
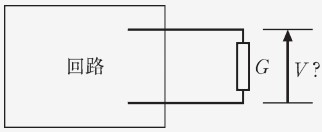
-
求めたい電圧が流れている枝路の抵抗を取り除き、その部分を端子とします。(この時点では、回路を開放したわけではありません。)

-
間を短絡し、端子間の短絡電流を求める。このとき、これまで学んだ定理などを利用する。
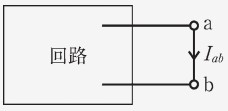
-
端子から見た回路の合成抵抗 、もしくは、コンダクタンスを求める。このとき、これまで学んだ定理などを利用する。
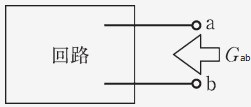
-
求めた短絡電流と抵抗より、端子 間につながれている抵抗 に流れる電圧 は、以下の式から計算できる。なお、枝路に抵抗がないときは とする。
適用例
電圧源を持つもの
以下の電圧源が 2 つ並列接続された回路を考えてみます。※回路自体は、テブナンの定理の適用例「電圧源を持つもの」で出てきたものと同一です。
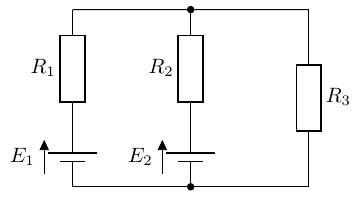
この抵抗に掛かる電圧を、ノートンの定理を用いて求めよ。キルヒホッフの法則でも計算ができますが、ノートンの定理を用いてみます。
-
求めたい電圧がかかっている枝路の抵抗を取り除き、その部分を端子とします。(回路を開放したわけではありません。)また、問題を解きやすくするために、などを定義します。
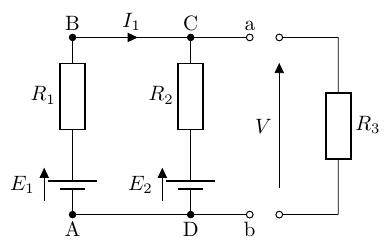
-
端子 間を短絡し、短絡電流を求めます。
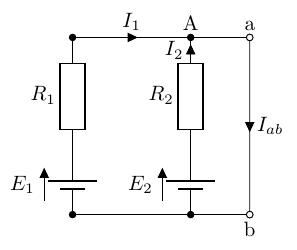
ここでは、キルヒホッフの法則を用います。- 点 A の電流:
- 外周の閉回路の方程式:
- 右側の閉回路の方程式:
- 以上より:
-
端子 間は短絡したままで、端子 間から見た回路の合成抵抗 を求めます。このとき、電圧源は短絡します。
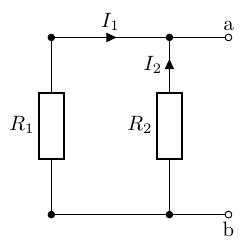
合成抵抗
※ ノートンの定理に代入しやすいように、を求めています。 -
抵抗 にかかる電圧 は、求めた短絡電流と抵抗をノートンの定理より以下のように計算できます。つまり、ノートンの定理: に、ここまで求めたとを代入します。
※ ここで求めたは、テブナンの定理で求めた電流に抵抗を掛けたものになっています。
電流源を持つもの
以下の回路の 4の抵抗に掛かる電圧を求めます。※回路自体は、テブナンの定理の適用例「電流源を持つもの」で出てきたものと同一です。
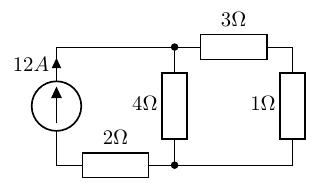
分流の法則 () とオームの法則 () から 24[V]と求められますが、ノートンの定理を用いてみます。
-
求めたい電流が流れている枝路の抵抗を取り除き、その部分を端子と定義します。
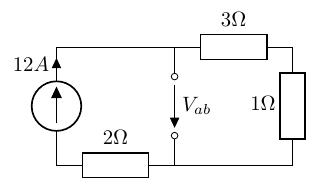
-
端子 間を短絡し、その部分の短絡電流を求めます。
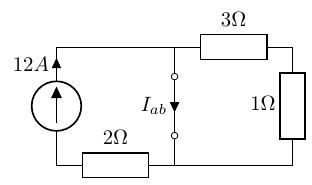
短絡しているので、12[A]がそのまま掛かります。 -
端子 間は短絡したままで、端子 間から見た回路の合成抵抗 を求めます。このとき、回路中の電流源は開放します。
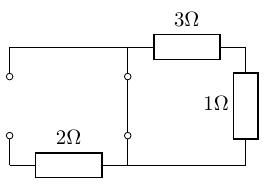
-
最後にノートンの定理: に、ここまで求めたとを代入します。
※ ここで求めた 4の抵抗に掛かる電圧[V]は、テブナンの定理で求めた開放電圧とは異なります。
演習問題
例題 4.5
次の回路でに掛かる電圧を求めよ。

例題 4.7
次の回路で端子間の電圧を求めよ。
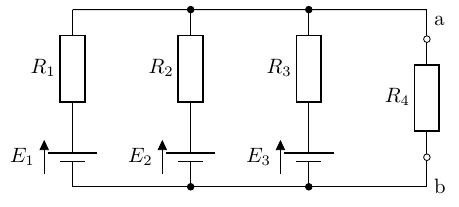
追加問題
問題A
次の回路の、抵抗にかかる電圧をノートンの定理で求めよ。
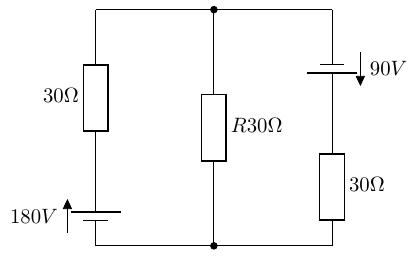
問題B
次の回路の、抵抗にかかる電圧をノートンの定理で求めよ。
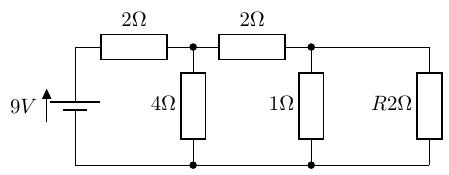
2つの定理の双対性
テブナンの定理とノートンの定理は双対関係にあります。具体的には、双対の関係となるものは、電流と電圧、抵抗とコンダクタンス、開放と短絡です。つまり、それぞれを入れ替えると片方の定理をもう片方の定理に変換可能です。
-
テブナンの定理:
-
ノートンの定理:
2 つの定理のイメージを説明した部分を比較してみても双対性が確認できます。ノートンの定理のイメージの説明では、簡単化のためにコンダクタンスを使っていませんので、抵抗はどちらの定理にも登場します。
-
テブナンの定理のイメージ
とある回路の抵抗に流れる電流を求めたいとき、その抵抗以外の部分の回路を抵抗と電圧の 2 つからなる等価な電圧源に変換し、そこからオームの法則で電流を求めます。また、端子 間に掛かる電流を求めたいので、2 点間を開放します。
-
ノートンの定理のイメージ
とある回路の抵抗に流れる電圧を求めたいとき、その抵抗以外の部分の回路を抵抗と電流の 2 つからなる等価な電流源に変換し、そこからオームの法則で電圧を求めます。また、端子 間に掛かる電圧を求めたいので、2 点間を短絡します。